De kritiek op DLE’s weerlegd
Gerard Melis
Orthopedagoog/gz-psycholoog, onderwijsadviseur en ontwikkelaar bij Boom Test Uitgevers
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/DLE-uitleg.php

Dit artikel is geschreven samen met Paul Oosterveld en Johan Schokker
Bezwaren tegen DLE’s
Hoewel er in het basisonderwijs veel wordt gewerkt met DLE’s, is er ook kritiek op het gebruik ervan. Maatgevend in de kritische perceptie van DLE’s is een artikel van Arne Evers en Wilma Resing (Evers & Resing, 2007). De titel van hun artikel liegt er niet om: ‘Het drijfzand van didactische leeftijdsequivalenten’. Evers en Resing brengen tien bezwaren tegen het gebruik van DLE’s naar voren. We geven steeds kort hun bezwaar weer en gaan daar vervolgens op in.
De gedachte dat de schoolvaardigheden bij leerlingen op lineaire wijze toenemen, is uiteraard van elke theoretische rechtvaardiging of praktische aanwijzing ontbloot; leerlingen kunnen onverwachte leersprongen doormaken, en ook tijdelijke (en in een enkel geval permanente) terugval vertonen. Schoolprestaties zijn afhankelijk van een gevarieerde reeks factoren, zoals de aanleg, de motivatie en het welbevinden van het kind, de sociaaleconomische status van het gezin, de kwaliteit van de leerkracht en het leermateriaal, enzovoorts. Over het belang van al deze factoren bestaat veel wetenschappelijke literatuur, maar over de wijze waarop al deze factoren met elkaar interacteren bestaan slechts vermoedens; de werkelijkheid van het schoolgaande kind is gewoonweg te complex. Er lijkt in elk geval weinig evidentie te bestaan voor de veronderstelling van een ‘regelmatige stabiele curve’.
Dit is echter ook geen veronderstelling van de toepassing van DLE’s. DLE’s zijn immers normscores. Ze pretenderen dan ook een beschrijving te geven van de norm en niet van het leertraject van de individuele leerling. Dat leerlingen op individueel niveau allerlei onregelmatige leercurves laten zien, sluit niet uit dat een lineaire ontwikkeling een goede beschrijving geeft van de gemiddelde leerling. De ‘gemiddelde leerling’ is een fictief construct, maar dat neemt niet weg dat het vergelijken van de prestaties op een toets van een individuele leerling met een dergelijk construct nuttig kan zijn.
Ook is het niet helemaal correct te beweren dat een DLE-schaal uitgaat van een strikt lineaire ontwikkeling, zoals Evers en Resing doen. Vaak is een toets namelijk op meerdere momenten in een schooljaar genormeerd. De interpolatie tussen de nomeringsmomenten gaat inderdaad uit van een lineaire toename, maar wanneer er ook halverwege het schooljaar normeringsgegevens zijn verzameld, hoeft de vaardigheidsbeheersing, en daarmee ook de onder de opgestelde DLE-schaal gepositioneerde normscores, niet perse lineair toe te nemen. In een DL/DLE-grafiek wordt de tijd als meeteenheid genomen – na een bepaald aantal maanden onderwijs verwacht men dat de gemiddelde leerling een daarbij behorende normscore behaalt – terwijl in de schaalgrafieken van de Cito LOVS-toetsen de vaardigheidsscore de meeteenheid is.
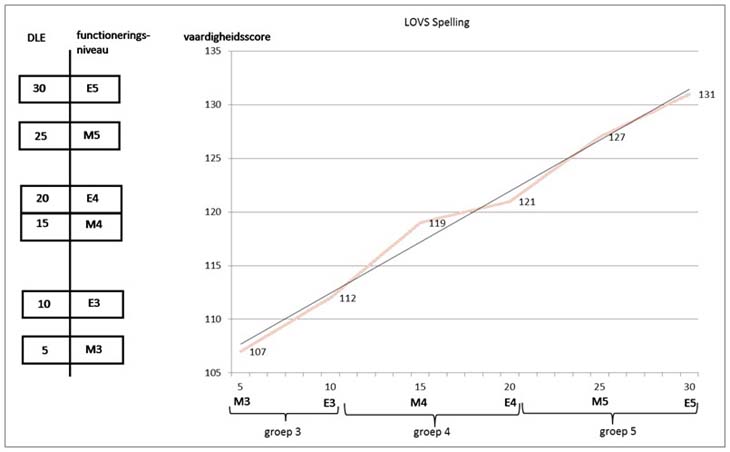
Uit dit voorbeeld blijkt ook dat de kwaliteit van een DLE-schaal afhankelijk is van het aantal normeringsmomenten. In bovenstaande voorbeeld beschikken we om de vijf maanden over normeringsgegevens. Interpolatie tussen de normeringsmomenten vindt wel plaats, maar als de perioden tussen de verschillende normeringsmomenten niet te groot zijn, is dit een aanvaardbare procedure. Zeker wanneer men bedenkt dat men bij het gebruik van percentielnormen ook dikwijls gedwongen is normen toe te passen buiten de eigenlijke normeringsperiode. Hierdoor kunnen vertekeningen optreden, maar die zullen gering zijn wanneer men niet al te zeer afwijkt van de normeringsperiode. Zo geldt ook voor een DLE-schaal dat interpolatie aanvaardbaar is, wanneer de afstand die is gelegen tussen de verschillende normeringsmomenten, niet te groot is.
Het is waar dat toetsen met een bodem- en/of plafondeffect niet kunnen differentiëren tussen respectievelijk zwakke of goede leerlingen. Maar het is de vraag of dit als een bezwaar kan gelden in het gebruik van DLE’s. Het optreden van bodem- en/of plafondeffecten duidt over het algemeen op een onjuiste toepassing van toetsen (bijvoorbeeld wanneer men een Rekenen-Wiskunde toets afneemt die veel te moeilijk is voor de leerlingen) of een slechte toetsconstructie. Een toets met een duidelijk bodemeffect is dan ook niet geschikt om zwakke leerlingen te differentiëren. Dat staat echter los van de DLE als normscore. Ook bij andere normscores, zoals de Cito-niveaus A tot en met E, treden problemen op in geval van bodem- en plafondeffecten.
Dat is een gelijksoortig bezwaar als bezwaar 2. Wanneer men bijvoorbeeld een schoolvaardigheidstoets die bedoeld is voor groep 4, afneemt bij een groep in de bovenbouw, kan men verwachten dat de meeste leerlingen een maximale score zullen behalen (plafondeffect). Het aantal fouten dat dan gemaakt wordt, is gewoonweg te klein om de leerlingen op betrouwbare wijze te kunnen differentiëren. Dit vertaalt zich ook in de DLE-schaal, waar in de bovenste regionen van de schaal ‘gaten’ vallen.
Overigens kan hetzelfde bezwaar gelden voor de wijze waarop het Cito toetsscores normeert: als de scores in de normgroep weinig verschillen, worden toch sommige leerlingen als A en anderen als E geclassificeerd, hoewel die classificatie gebaseerd is op kleine verschillen.
Wanneer kleine scoreverschillen leiden tot aanzienlijke verschillen in DLE’s, is dat dus een aanwijzing dat de toets in dat scoredomein niet voldoende differentieert. Meestal betekent dat, dat de toets te moeilijk of te makkelijk is voor de betreffende leerlingen.
In sommige situaties vindt men het wenselijk normscores door te trekken naar een lager of een hoger leerjaar door middel van extrapolatie. Dit is echter een hachelijke praktijk; er zijn ter ondersteuning namelijk geen toetsgegevens beschikbaar. Men neemt in deze situaties aan dat de lineaire toename van de vaardigheidsbeheersing zich voortzet, zonder dat daarvoor voldoende empirische evidentie beschikbaar is. In de tabellen zoals die in het DLE Boek worden gepresenteerd, komt deze praktijk dan ook niet voor. Dit kan dus niet als een algemeen geldend argument tegen DLE’s worden opgevoerd.
De DLE-schaal is ontworpen voor het basisonderwijs. Het voortzetten van de schaal na de overgang naar het voortgezet onderwijs is vooral twijfelachtig wanneer de schaal is opgesteld door middel van extrapolatie. In de praktijk scoren leerlingen van het eerste leerjaar vmbo op bijvoorbeeld de Tempo Toets Rekenen van Teije de Vos op een DLE rond de 40 en 50, dus op het niveau van leerlingen uit groep 6 en 7 van het basisonderwijs. Hoewel de toets niet specifiek voor deze groep is genormeerd, kan men niet beweren dat een dergelijke normscore niet inzichtelijk is; een lwoo-leerling blijkt dan het niveau te hebben van een leerling uit groep 5. In het ideale geval beschikt men ook over percentielscores, zodat naast de leerachterstand van de leerling ten opzichte van de gemiddelde basisschoolleerling, ook kan worden bepaald hoe erg dat is in vergelijking met leerlingen van het eigen onderwijsniveau.
DLE’s zijn gebaseerd op gemiddelde en/of mediane scores (de mediaan geniet de voorkeur want deze is minder sterk afhankelijk van extreme waarden) op de verschillende normeringsmomenten; over de spreiding wordt geen vooronderstelling gedaan.
Er is ook geen directe relatie tussen percentielscores en DLE-scores. In dit verband halen Evers en Resing een voorbeeld van Geelhoed en Reitsma aan over het PI-dictee. Het PI-dictee is een spellingstoets voor het basisonderwijs, die kan worden afgenomen vanaf groep 3. In groep 3 kunnen de leerlingen nog niet zoveel woorden schrijven, dus valt de ruwe score relatief laag uit. We veronderstellen nu dat we het PI-dictee in januari bij leerlingen uit groep 3 afnemen en in de daarop volgende drie leerjaren nemen we nogmaals deze zelfde toets af.
Dit levert voor leerling A en leerling B de volgende scores op (zie tabel 3, Geelhoed en Reitsma, p. 30-31).
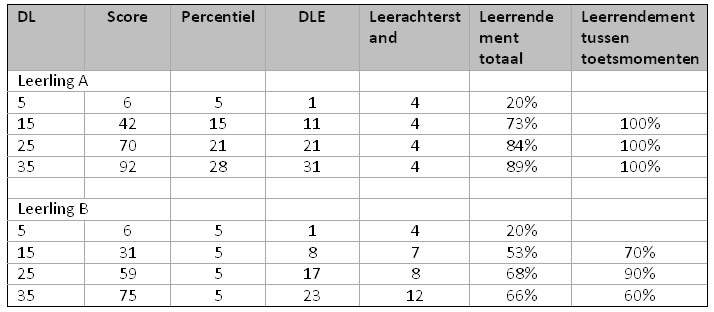
Het kritiekpunt is nu dat wanneer men uitsluitend oog heeft voor de leerachterstand, bij leerling A de indruk ontstaat dat er geen verbetering van de leerprestaties heeft plaatsgevonden. Zijn leerachterstand blijft immers dezelfde.
Wanneer men bij de interpretatie van de normscores ook de percentielscores betrekt, is dat zeker inzichtelijk. Daaruit blijkt dat leerling A van een relatief slechte leerling zich op het PI-dictee heeft verbeterd tot een bijna gemiddelde leerling. Deze relatieve positieverbetering ten opzichte van de medeleerlingen is niet direct af te leiden uit de DLE-score.
Daar staat tegenover dat wanneer men uitsluitend gebruik maakt van percentielscores, dit ook zijn beperkingen kent. Dit blijkt uit het voorbeeld van leerling B, dat eveneens door Geelhoed en Reitsma wordt gegeven. Leerling B behaalt steeds een percentielscore van 5, en daaruit is moeilijk af te leiden of deze leerling ondanks zijn constante percentielscore zich in de spelling heeft verbeterd. Leerling B is een zwakke leerling, maar door te kijken naar de DLE’s wordt duidelijk in hoeverre hij zich in het spellen heeft verbeterd en krijgt men inzicht in zijn leertempo. Wanneer men uitsluitend naar de percentielscores kijkt, zou men gemakkelijk het idee kunnen krijgen dat deze leerling stil is blijven staan. De DLE’s van leerling B maken duidelijk dat hij wel degelijk vooruit gaat, hoewel zijn leerachterstand in de loop der jaren is toegenomen.
Het idee van Evers en Resing dat een leerachterstand van een leerling in termen van DLE’s ook aangeeft wat de benodigde leertijd van de leerling zou zijn om de betreffende achterstand in te halen, berust op een misvatting. De DLE’s doen onder meer een uitspraak over de gemiddelde leerachterstand van een leerling; het gebruik ervan is vooral nuttig om te bezien, aan de hand van de toetsresultaten van een leerlingvolgsysteem, of de eventuele leerachterstand toe- of afneemt. Zoals eerder aangegeven, kan een leerachterstand uitgedrukt in DLE’s niet direct worden vertaald in het aantal maanden onderwijs dat een specifieke leerling nodig zou hebben om die achterstand in te halen; dat hangt geheel van de betreffende leerling af en zijn of haar omstandigheden.
Volgens Evers en Resing wordt het gebruik van DLE’s vertroebeld door onzuiverheid van de normgroep, waarin immers ook gedoubleerde leerlingen zijn opgenomen. Zoals hierboven aangegeven, dient de DL te worden begrepen als het aantal onderwijsmaanden dat de gemiddelde leerling op dat specifieke moment heeft genoten. Dat moment correspondeert met een gemiddeld onderwijsniveau in de normgroep. Gedoubleerde leerlingen maken altijd deel uit van de populatie basisschoolleerlingen in een bepaald leerjaar en moeten daarom ook niet buiten de normgroep worden gehouden.
Toetsontwikkelaars zoals het Cito sluiten voor de bepaling van het niveau A t/m E gedoubleerde leerlingen evenmin uit; zowel daar als bij de daaraan ontleende DLE-schaal is sprake van ‘onzuiverheid’ van de normgroep.
Overigens, wanneer men te maken heeft met een gedoubleerde leerlingen wordt meestal aangeraden de DL van zo’n leerling aan het begin van het leerjaar tien maanden terug te zetten. De leerling presteert immers op het onderwijsniveau waarin hij wordt onderwezen, en ook het toetsen vindt plaats op dat niveau. Men is geïnteresseerd in hoeverre een leerling de onderwezen leerstof beheerst, en het zou niet terecht zijn voor een gedoubleerde leerling een maatstaf te hanteren van een klas hoger; hij is immers niet voor niets gedoubleerd.
Om een volledige DLE-schaal op te stellen, dient een toets inderdaad uit ten minste 60 opgaven te bestaan. Dit is in de regel niet het geval, omdat een toets zelden is bedoeld voor alle leerlingen van het basisonderwijs, en in de praktijk de afnameperiode van een toets beperkt is. De DLE-schaal wordt dan ook in de praktijk meestal opgesteld voor een beperkt domein, wat betekent dat men de toetsscore maar met een beperkt aantal DLE’s kan verbinden. Voor het overgrote deel van de gevallen voldoet een dergelijke schaal ook.
Bovendien speelt het probleem niet wanneer, zoals bij het Cito LOVS, de toetsen voor de verschillende leerjaren op één vaardigheidsschaal worden gezet door middel van itemrespons-technieken.
Zoals al eerder aangegeven, dient men precies te zijn in de interpretatie van een DLE. Het is duidelijk dat men geen uitspraak kan doen over een toetsinhoud die ook niet getoetst wordt. Dat scholen verschillen in de tijd waarop ze bepaalde lesstof aanbieden, is voor gebruik van DLE’s niet relevant, maar betreft het verschil tussen methodegebonden toetsen en methodeonafhankelijke toetsen.
Besluit
“Leerlingen met een achterstand behalen meestal een vaardigheidsniveau E of V. Deze niveauaanduiding zegt niets over de groei die zij doormaken. Daarom staat in het alternatief leerlingrapport de ontwikkeling van de vaardigheidsscore in de tijd centraal.”
Wat de critici van DLE’s kan worden verweten, is dat ze blijkbaar zo content zijn met hun manier van kijken dat ze geen of weinig aandacht hebben voor het feit dat de meeste leerkrachten graag (ook) op een andere manier naar de gegevens kijken. Een manier van kijken waarmee ook inzichtelijker aan de ouders over de leerontwikkeling van hun kinderen verslag kan worden gedaan. Het is zeker niet zo dat de ene manier beter is dan de andere: het hangt er vanaf waar je naar wilt kijken. Om sommige zaken te zien moet je op een bepaalde manier kijken, om andere zaken te zien moet je op een andere manier kijken. Dat blijkt bijvoorbeeld uit het besproken voorbeeld van de twee leerlingen van het PI-dictee, dat Geelhoed en Reitsma juist aandragen als een argument tegen het gebruik van DLE’s.
Feit is dat leerkrachten het gebruik van DLE's in het algemeen nuttig vinden, dus graag op ook die manier naar de gegevens kijken.
Literatuur
Cito. (2012). Alternatief leerlingrapport.
Cito. (2012). Ontwikkelingsperspectief vaststellen op basis van vaardigheidsscores.
Cito. (2012). Toetsscore, vaardigheidsscore… en dan?
Gerard Melis. (1995 en later). DLE Boek. Amsterdam: Boom test uitgevers.
Gerard Melis. (2012). DLE Schalen indicatiestelling LWOO en PrO voor instroom in schooljaar 2013-2014. Amsterdam: Boom test uitgevers.
Henriëtte de Groot, Marjan Huizing en Anneke Noteboom. (1999). Leerlingvolgsysteem en speciale leerlingen. Arnhem: Cito.
Jan Geelhoed en Pieter Reitsma. (2004). PI-dictee. Amsterdam: Pearson.
G.N. Melis en F.R. Sonsma. (1989). Het SAVU-leerlingvolgsysteem. Functie-Opzet-Invoering. Hoevelaken: Christelijk Pedagogisch Studiecentrum.
G.N. Melis. (1991). DLE en leerling volgsysteem. Ja, nee... toch maar; of… juist wel doen?! School & Begeleiding, 29, 71 -79.
A.H.J. Moelands, M.J.C. Mommers en J.H.L. Oud. (1990). Leerlingvolgsystemen verklaard en vergeleken. School & Begeleiding, 26, 19-28.
J.H.L. Oud en M.J.C. Mommers. (1990). De valkuil van het didactisch leeftijdsequivalent. Tijdschrift voor Orthopedagogiek. 29, 445-459.
Teije de Vos. (2007). Schoolvaardigheidstoets Technisch Lezen. Amsterdam: Boom test uitgevers.
Teije de Vos. (2012). De geschiedenis van de DLE's. http://testen-en-toetsen.blogspot.com/2012/04/de-geschiedenis-van-de-dles.html
Toetsen voor speciale leerlingen. Voor groep 3, 4 en 5. Arnhem: Cito.
Over de auteurs
Paul Oosterveld is methodologisch en psychometrisch adviseur. Hij was vijf jaar werkzaam als universitair docent bij de UvA en is auteur van de d2 Aandachts- en concentratietest voor kinderen.
Johan Schokker is werkzaam als methodoloog bij Boom test uitgevers.
Dit artikel verscheen in verkorte vorm in het septembernummer van het Tijdschrift voor Remedial Teaching (jaargang 20, 2012, nummer 4, pp. 30-33) en in deze vorm in Aanvulling oktober 2012 van Gerard Melis. (1995 en later). DLE Boek. Amsterdam: Boom test uitgevers.