Automatiseren met telraam en getallenlijn
Leonard Verhoef
Directeur bij Human Efficiency
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/tellend-optellen-getallenlijn.php

In groep 3 en 4 tellen kinderen nog wel op hun vingers. Ook worden het telraam en de getallenlijn gebruikt. Sommige kinderen blijven te lang op hun vingers tellen.
Dat tellen leidt tot vinger-, oog- en werkgeheugenfouten. Dat zijn géén rekenfouten. Verder leidt een foute uitkomst achter een opgave niet tot automatisering van die opgave.
Wat doen de vingers, de ogen, het werkgeheugen en het denken tijdens dat getel?
1 Pasvorm voor de vingers
Concrete materialen zijn belangrijk bij het leren rekenen. Deze materialen moeten de vingers dus goed passen om vingerfouten te voorkomen. Dit geldt vooral voor zevenjarigen die nog geen goede fijne motoriek hebben. De handeling moet verder snel uitgevoerd kunnen worden zodat deze verkortbaar is tot een mentale handeling.
1.1 Grip voor de vingers
De gebruikelijke telramen hebben gladde ronde kralen. Dat is prettig voor kralen om je nek. Maar de vingers hebben minder grip op rond en glad. 'Grip' is een bekend probleem in de toegepaste psychologie. Bij de komst van personal computers ontwierpen ergonomen het toetsenbord (afb. 1). Dat toetsenbord was zeer hand-, vinger- en vingertopvriendelijk met onder andere holle, ruwe oppervlakken en een goed hoorbare en voelbare feedback (Verhoef, 1984). Blindtypers konden daar 600 aanslagen per minuut mee halen. De toetsen van de huidige laptops zijn meer vlakke afgesleten Belgische kasseien (afb. 2).


Ook de kralen op telramen moeten een goede grip hebben. Telramen voor professionals hebben grip doordat de kralen schijven zijn met een wat scherpe rand (afb. 3). Door de schijfvorm passen er meer kralen in het oogfixatieveld. Ook is de af te leggen afstand tussen de kralen kleiner. Getallen worden daardoor niet kraal voor kraal geschoven maar in één geautomatiseerde motorische handeling met meer vingers (akkoordaanslag) tegelijk op hun plaats getikt.

1.2 Verkorten van de handelingen met de vingers
Tellend optellen is een motorische handeling met vinger-, oog- en stemspieren. Wanneer je de spieren verlamt dan kun je niet meer tellen. Het motorische beeld is tijdens het tellen een rij identieke huppels. Ratten laten zien hoe een rij motorische huppels geautomatiseerd worden. Zij blijken in een doolhof vooral op hun motorisch geheugen te navigeren. Train je ze goed op een doolhof dan wordt het verstand uitgeschakeld. Verander je na de training dan stiekem een hoek dan nemen ze de verdwenen hoek toch en knallen ze zonder aarzelen tegen de goed zichtbare nieuwe muur (Dudchenko, 2010).
Ook de (op)telhandeling wordt een motorische reflex. Soms zie je dat bij kinderen. Toon je een opgave dan bewegen de vingers in een reflex, het kind kijkt zeer kort naar zijn vingers en snel komt er een antwoord. De telreflex kan zo snel zijn dat jij en de toets aan de reactietijd niet zien dat het kind telt. Niets aan de hand is dan de conclusie. Als je dus gaat oefenen, oefenen, oefenen, zoals men wel adviseert, ontwikkelt het kind dus een motorische reflex en geen inzicht in de structuur van de getallen.
Motorische reflexen zijn moeilijk af te leren. Ga maar eens in een auto rijden waar de rem- en het gaspedaal verwisseld zijn. Dat is dodelijk. Het kind mist met dat vingertellen ook de lessen die leren hoe je anders dan tellend kunt optellen. Dat is dodelijk. Voor het denkend rekenen. Ook zijn de ongestructureerde repeterende motorische handelingen niet mentaliseerbaar. Sommige creatieve vingertellers proberen nog structuur aan te brengen door vierkantjes op hun bovenbeen te tikken. Heel slim. Dat voorkomt telfouten en de juf ziet het vingertellen niet. Maar het is nog steeds onverkortbaar motorisch tellen. En het kind. Tja, niets aan de hand. Dat zit twee jaar lang te vingertellen. Niet echt uitdagend zou je zeggen. Tot de sommen boven de 20 komen .... Dan is er ineens wel een uitdaging.
2 Pasvorm voor de ogen
Niet alleen de vingers zijn nodig voor tellen. Ook de ogen doen mee. Wat vinden die van lijnmaterialen als het telraam en de getallenlijn?
2.1 Het oogfixatieveld
Het oogfixatieveld is een cirkel, een beetje ovaal (15°). Dat veld heeft veel receptoren en dient voor nauwkeurige identificatie (afb. 4). Zoogdieren zijn namelijk al miljoenen jaren geen brievenbuskijkers maar patrijspoortkijkers. Brievenbuskijken is namelijk dodelijk. Een brievenbuskijker ziet een tijger die linksonder nadert niet aankomen. Ook is in afbeelding 4 te zien dat geschreven teksten de ogen eigenlijk niet zo goed passen.

Het effect van essentiële informatie die buiten het oogfixatieveld ligt, is te zien in de onmogelijke afbeelding 5. Afbeelding 6 toont hetzelfde figuur maar dan verkleind en wel zo dat alle noodzakelijke informatie wél in het oogfixatieveld past. Dan is onmiddellijk wél te zien waarom afbeelding 5 niet kan.


Cognitief psychologen hebben veel onderzoek gedaan naar de vraag: Hoe moet je twee getallen die bij elkaar horen tonen? Je kunt ze horizontaal naast elkaar zetten of horizontaal onder elkaar. Verticaal onder elkaar of naast elkaar kan ook. Diagonaal geplaatst zou ook kunnen. En natuurlijk combinaties van dat alles (afb.7).
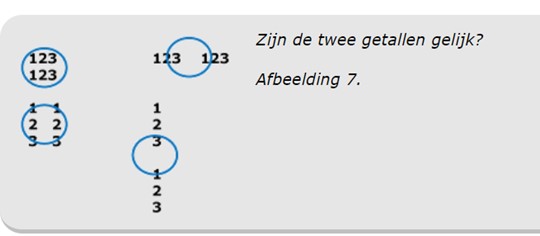
De vraag 'Waar zet je de twee getallen neer?' leverde veel wetenschappelijke onderzoeken en publicaties op. Met één psychologische klap beëindigde Woodward (1972) het debat: Maakt niet uit. Bepalend is de afstand tot het oogfixatiepunt. Vlak bij elkaar, bij het oogfixatiepunt, hoe dan ook, leidt tot snellere en foutlozer performance dan uit elkaar. Datzelfde cognitief psychologische gemillimeter geldt natuurlijk ook bij rekenmaterialen zoals in afbeelding 8 te zien is. Je moet bij die afbeelding dan overigens anders kijken dan de evolutie je laat kijken. Brievenbuskijkers zouden wel in één keer zien wat er aan de hand is.

Afbeelding 9 toont een ander rekenvoorbeeld. De groene bal boven wordt vaker over het hoofd gezien dan een bal die vrijwel op het fixatiepunt ligt, zoals in afbeelding 10. Vraag je aan kinderen: Hoeveel ballen zijn er? dan verschilt de performance tussen de centrische en de excentrische groene ballen dan ook.

2.2 Markant
De ogen en de hersenen zijn al miljoenen jaren zeer geïnteresseerd in afwijkingen van patronen. Anders dan normaal betekent immers: mogelijk dodelijk gevaar. Het effect van minder markant blijkt uit teksten in hoofdletters. Woorden met hoofdletters geven saaie rechthoekige patronen. Je kunt daardoor minder woorden per oogfixatie lezen. Stokken en staarten in woorden maken het woordpatroon markant. Door dit gemillimeter lezen kleine letters zo'n 10% sneller (Tullis, 1983). Ook het tekstbegrip neemt dan toe en de belasting van het werkgeheugen neemt af. Professionele tellers weten dat je met een markante ordening zónder tellen een aantal sneller en foutlozer kunt bepalen dan met een lijnordening (afb. 11).

Hoe zit dat met markante punten op het telraam en de getallenlijn? Deze hebben eigenlijk maar twee markante punten: het begin en het eind. Maar die punten zijn bij het rekenen zelf vrijwel niet nodig. Een aantal van 10, ook een nette rij van 10 (niet de plaats van 10) en zelfs het aantal 5, is visueel dan niet direct identificeerbaar als 5 (subitizable, Clements, 1999). Dat is ook te zien in afbeelding 8. Je moet wéten dat het er 5 zijn. De groep kralen is dus een symbool dat staat voor het aantal 5.
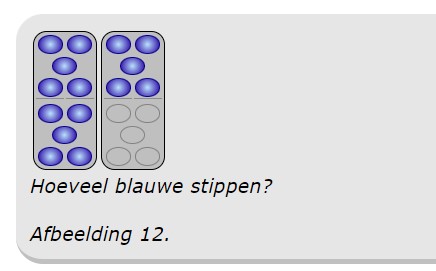
Niet identificeerbaar vindt de evolutie gevaarlijk. Dat kan dodelijk zijn. De evolutie dobbelt liever. Je kunt niet niet zien wat het aantal stippen van afbeelding 12 is.
3 Pasvorm voor het werkgeheugen
3.1 Een chaotisch vergiet
De ogen hebben een oogfixatieveld: de visuele focus. Het geheugen heeft ook zo iets: het werkgeheugen. Het werkgeheugen is de mentale focus. Onhandig is dat het werkgeheugen eigenlijk een nogal chaotisch vergiet is. En ook nog klein. Er kunnen zo'n zeven elementen in zegt men wel. Blind valt nog wel te leven. Als het werkgeheugen niet meer werkt dan is leven wel erg moeilijk. Dat blijkt wel uit ziekten die het werkgeheugen aantasten.
Het kleine en tamelijk onbeheersbare werkgeheugen koppelt wat het oogfixatieveld, het langetermijngeheugen en vooral de emotie er in stort. Het werkgeheugen is daarmee de plek waar het eigenlijke denken en rekenen plaatsvindt concluderen Coolidge en Wynn (2018) in een nogal uitvoerige en grondige neurologische en antropologische studie. In het werkgeheugen openbaart zich dan: inzicht, een geniaal idee, onzin of een grap.
Baddeley had in 1987 het werkgeheugen al fors op de psychologische kaart gezet. Deze cognitieve psychologie sluit aan bij het onderzoek naar de relatie tussen werkgeheugen en rekenen. Uit neurologisch onderzoek blijkt dat het werkgeheugen bij kinderen die rekenen, harder werkt dan bij volwassenen (Nieder, 2019). Veel onderzoekers constateerden een verband tussen het werkgeheugen en reken-vaardigheid op jonge leeftijd en later (De Vita, 2021). Ook blijkt dat dyscalculie samengaat met defecten in het werkgeheugen (Nieder, 2019). Om goed te kunnen rekenen heb je meer aan een goed werkgeheugen dan aan intelligentie concluderen Alloway & Alloway (2013) verder.
Duidelijke taal allemaal. Althans, dat het werkgeheugen belangrijk is. Maar het werkgeheugen staat bij het rekenen nog niet zo goed op de kaart (LeFevre et al., 2005). Ook in 2024 niet. Wat je nu precies wél moet doen en vooral wat niet moet doen, dat is niet zo duidelijk in de rekenliteratuur.
3.2 Tellend optellen en het werkgeheugen
Wat betekent het werkgeheugen concreet voor het tellend optellen? Bij het tellend optellen moet in het werkgeheugen: de twee termen van de opgave en de opdracht: optellen. Verder is nodig: de telwoordenrij en welk telwoord je gehad hebt. Inmiddels begint het kleine werkgeheugen wel vol te raken. Vooral als het gaat om 'rekenzwakken'. Eventuele stress verkleint het werkgeheugen meestal ook wel flink. Hier ging het alleen nog over optellen. Bij het aftrekken zal die belasting niet minder zijn. Er is dan nog maar weinig ruimte over om de essentie, namelijk de relevante getalstructuren, te kunnen "zien". Vooral als de telmiddelen die getalstructuren niet goed tonen.
3.3 Het werkgeheugen en het vingertellen
Een probleem bij het vingertellen is de vingers in de goede stand zetten. Fijnmotorische handelingen zijn nog niet goed ontwikkeld bij zevenjarigen. Die handelingen kosten tijd en aandacht. Daardoor is er meer kans dat er wat uit het werkgeheugen ontsnapt.
-
Wanneer één term op de ene hand past en de andere term op de andere hand dan is de interpretatie eenvoudig. De afzonderlijke handen zijn een geheugensteun voor de termen. Maar als één van de termen meer of minder dan 5 is, dan loopt deze over de handen heen. Waar hoort welke vinger ook al weer bij? Reken zelf 4+3 maar eens op je vingers uit. Incompatibiliteit is vragen om problemen weet de toegepaste cognitieve psychologie. Op een kaart op straat moet links op de kaart ook links van de lezer zijn. Door incompatibiliteit tussen termen en handen is de opgave 3+4/4+3 waarschijnlijk moeilijker dan 5+4/4+5. 5+4 is gewoon een duim omlaag. Ondanks dat bij 5+4 het aantal te tellen eenheden 2 meer is. Dat blijkt ook uit de statistiek.

- Ook krijgt één vinger bij het vingertellen een dubbeltaak, namelijk tellen en aanwijzen. Het vingerbeeld is dan nog ingewikkelder.
- Bovendien zal de motoriek meer bepalen welke vingers je opsteekt dan een goede visuele afbeelding. Steek maar 3 vingers op. Je slaat dan de eerste vinger, de duim over.
- Doordat je voor hetzelfde aantal verschillende combinaties van vingers kunt opsteken, zijn er meer vingercombinaties mogelijk voor hetzelfde aantal. Als je woorden steeds met andere letters schrijft dan schiet het leren lezen niet op. Met steeds andere vingerconfiguratie voor hetzelfde aantal moet het kind dus wel blijven tellen (letter voor letter lezen).
- En dan tot slot moet het werkgeheugen ook de optelprocedure sturen.
Dat vingertellen belast het werkgeheugen dus flink. Je kunt het vingertellen verbieden. Dat is gemakkelijk, voor de leerkracht. Ook adviseert men wel oefenen, oefenen, oefenen met werkbladen. Dan wordt wel de motorische telreflex verder ingesleten. Dat wil je eigenlijk juist niet. Je kunt ook kiezen voor wat je wél wilt: Opgaven oplossen door gebruik te maken van de getalstructuur. Dat kan ook wel met de vingers maar dan moet je de opgavestructuur niet mét de vingers tonen maar óp de vijf-tallige vingerstructuur (afb. 13).
De afzonderlijke termen, de uitkomst en zelfs de splitsing rond 5 (4+3=4+1+2) zijn dan tegelijk in het oogfixatieveld aanwezig en tegelijk identificeerbaar. Dus geen werkgeheugenbelasting en geen getel. Ook vrijwel geen interpretatieproblemen. Verder kunnen kinderen vast wennen aan het splitsen van getallen om het optellen te vereenvoudigen, bijvoorbeeld bij het over 10 gaan. Oh ja, als je je handen aan je buur toont vraag dan even: Welke opgave is dit? Je hebt dan namelijk een 'omdraaier'. En natuurlijk: Wat is de uitkomst van jouw opgave?

3.3 Het werkgeheugen en het telraam en de getallenlijn
Het vingertellen belast dus het werkgeheugen. Geldt dat ook voor strakke lijnmiddelen als het telraam en de getallenlijn? Een strakke rij kralen of getallen geven minder belasting van het werkgeheugen dan uit het hoofd tellen en op de vingers tellen. Optellen met een steun zoals in afbeelding 14 geeft 5% meer goede antwoorden dan optellen uit het hoofd of met de vingers. Je ziet eenheden minder gemakkelijk over het hoofd.


4 Pasvorm voor het denken
Als het kind nog volgorde-denkt en telt, dan is over 10 gaan bij 5+6 geen probleem. Gewoon ééntje verder tellen. Net als van 8 naar 9. De opgave 5+6/6+5 is voor het kind verder mogelijk eenvoudig omdat het een 'bijna tweeling' opgave is. Die zijn al bij het automatiseren onder 10 aan de orde geweest.
Vreemd is wel dat er bij 10 en 11 twee cijfers voor één getal zijn. Maar bij het lezen heb je ook twee letters voor één klank, zoals bij de klank ui. De letters zijn immers op. Bij de getallen zijn de cijfers niet op maar gaat het om tientalligheid en plaatswaarde. Ook de telwoorden reppen niet van tientalligheid en plaatswaarde. Aan tien is ook niets te horen dat wijst op tientalligheid. En bij 30 is dat ook niet. De 3 zit verborgen onder 'der' en 10 verbergt zich onder 'tig'. Kortom, de opgave 5+5 is gewoon 10 en eenvoudig: (97% goed en 3.9 sec., gr. 3&4). En bij 5+6 moet je gewoon ééntje meer tellen, pakweg 2 seconden meer teltijd. Zou je zeggen.
Echter, tellers hebben voor 5+6 niet pakweg 2 seconden méér nodig maar 15.5 seconden. Ook het aantal goede antwoorden is minder: 35%. Dat is toch wel gek. Het lijkt er op dat de kinderen wél in de gaten hebben dat er bij 10 wat aan de hand is. En de getallenlijn die toch zo'n jaar lang aan de muur hangt, heeft die het in de gaten? Hoe dan ook, hoe los je dat op?
4.1 Met pijlen
Een oplossing voor het over 10 gaan bieden pijlen op de getallenlijn (afb. 15).

Goed nieuws is dat de psychologie wel weet hoe pijlen werken. De pijlen zijn abstracte symbolen. Met pijlen ga je dus iets abstracts (tientalligheid, plaatswaarde, inwisselen) uitleggen met abstracte symbolen. De voorkeur van de leerpsychologie is: Leg iets abstracts uit met concréét materiaal. De cognitieve ontwikkelingspsychologie zegt ook zo iets. Het denken van zeven- en achtjarigen is volgens de cognitieve ontwikkelingspsychologie intuïtief en sterk afhankelijk van de waarneming (Mussen et al. 1970, Piaget, 1969).
Er zijn verder wat harde cijfers. Geef je volwassenen een verkeersbordencursus, daarna een examen en na het slagen toestemming om te gaan autorijden dan zien die volwassenen de geleerde borden regelmatig in de praktijk. Klaar is Kees zegt het CBR. Maar het blijkt dan dat 78% van die gediplomeerde ervaren automobilisten niet begrijpt wat het bord met pijlen van afbeelding 16 betekent (Verhoef, 2013).

Dus liever geen abstracte symbolen als pijlen voor de kinderen. Al met al is het dus ook heel begrijpelijk dat de 'rekenzwakke' leerling van afbeelding 15 niet kiest voor de pijlen maar voor de methode die de ervaren teller goed kent en die jij niet wilt: tellen.
4.2 Zonder pijlen
Het kan ook zonder pijlen. Geef je proefpersonen een bord dat cognitief psychologisch uitgemillimeterd is (afb. 17) dan krijg je zónder cursus, examen en praktijkervaring 56% meer goede antwoorden dan met het gebruikelijke bord mét cursus, mét examen en mét ervaring. Met name bij kinderen. Met name ook bij borden voor ingewikkelde en gevaarlijke situaties zoals spookrijden (Verhoef, 2011). De volgende vraag is natuurlijk: Kun je met cognitief en psychologisch uitgemillimeterd materiaal ook beter inzicht geven in het over 10 gaan? Ja, dat kan.

5 Pasvorm van de evolutie
Toch wel wat vreemd allemaal, dat tellen. We leren kinderen met lijnmaterialen een motorische huppelreflex aan om ze mentale rekenhandelingen te leren uitvoeren in een abstracte meerdimensionale getallenstructuur. Je leert kinderen dus eigenlijk dus dammen op een ganzenbord. De materialen die we daarbij gebruiken passen de ogen, het werkgeheugen, het denken en de getallen niet.
Die frictie tussen tellen en mensen is overigens begrijpelijk. Dat tellen is niet zo relevant voor de hoofdtaak van de ogen, het werkgeheugen en het denken, namelijk survival. Natuurvolken en zoogdieren tellen volgens ANS (approximate number system): Een, twee, drie, veel. Vier aanstormende wolven is evenveel als vijf: Wegwezen! Maar ja, stamhoofden wilden belasting heffen. Priesters wilden weten wanneer het precies zonnewende is. Ja, dan moet je gaan tellen. Zou je die evolutionaire totaalreflex Wegwezen! ook kunnen toepassen op het leren automatiseren van opgaven onder 10? Ja, dat kan. Dat is het volgende verhaal.
Voetnoten
- Je ziet niet dat de aantallen kralen niet kloppen.
- De statistieken komen van individuele bijlessen voor 'rekenzwakke' kinderen van twee Utrechtse scholen. Alleen de moeilijkste optelopgaven werden getest. Dus geen opgaven met 1 als term en 2-lingen. Meestal geeft het kind mondeling het antwoord en typt de proefleider het antwoord in. Met name bij grote getallen schrijven de kinderen het antwoord op papier en typt de proefleider het antwoord in. Op deze wijze verstoren de telwoorden de meting niet.
Literatuur
- Alloway T, & R. Alloway, (2013). The Working Memory Advantage. Train Your Brain to Function. New York etc: Simon & Schuster paperbacks.
- Baddeley, A., (1987). Working memory. Oxford: Oxford University Press.
- Campbell, J. (2005). Handbook of mathematical cognition. New York and Hove: Psychological Press.
- Clements, D.H. (1999). Subitizing: What Is It? Why Teach It? Teaching Children Mathematics, March 1999. www.researchgate.net/publication/258933161-Subitizing-What-Is-It-Why-Teach-It
- Coolidge, F. & Wynn, T., (2018). The Rise of Homo sapiens, The Evolution of Modern Thinking. Oxford: University Press.
- De Vita, Chiara, Costa, H.M., Tomasette, C. & Passolunghi, M.C. (2021). The contributions of working memory domains and processes to early mathematical knowledge between preschool and first grade. Psychological Research https://doi.org/10.1007/s00426-021-01496-4
- Dudchenko, P.A., (2010). Why People Get Lost. The psychology and neuroscience of spatial cognition. Oxford: University Press.
- LeFevre, J., DeStefano, D., Coleman, B. & Shanaham, T., (2005). Mathematical Cognition and Working Memory. In: Campbell: Handbook of mathematical cognition.
- Mussen, P.H., Conger, J.J. & Kagan, J., (1970). Child Development and Personality. New York, etc.: Harper International. Pag. 305.
- Nieder, A., (2019). A Brain for Numbers. The Biology of the Number instinct. Cambridge: The MIT Press.
- Piaget, J. (1969). Zes psychologische studies. Deventer: Van Loghum Slaterus.
- Tullis, T.S. (1983) The Formatting of Alphanumeric Displays: A Review and Analysis. Human Factors, Vol.25, no 6, pag. 657-682.
- Verhoef, L.W.M. (1984). Vinger-vriendelijke toetsen. Kantoor en efficiëncy. Vol. 23, no 3, pag. 17-25. https://www.humanefficiency.nl/gui/vinger-vriendelijke-toetsenborden.php
- Verhoef, L.W.M. (2013). Plaatsbepaling, hoe teken je pijlen en richtingen? https://www.humanefficiency.nl/icon-design/richting.php
- Verhoef, L.W.M., (2011). Complex signs increase wrong way driving. Simple signs decrease wrong way driving. In: Tec, Vol. 52 no 6, June 2011 , pag. 269-270. https://www.humanefficiency.nl/public/wrong-way-driving-signs.php
- Woodward, R.M. (1972). Proximity and Direction of Arrangement in Numeric Displays. Human Factors, vol. 14, no 4, pag. 337-343.