Anders beginnen met vermenigvuldigen en delen
Dolf Janson
Senior onderwijsadviseur en -ontwikkelaar bij Jansonadvies
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/beginnen-vermenigvuldigen-delen.php

De kans is groot dat je bij het woord ‘vermenigvuldigen’ eerder denkt aan ‘tafels’ dan aan delen. Dit is een van de redenen om de introductie van vermenigvuldigen en delen nog eens onder de aandacht te brengen. Het wordt tijd om dit anders aan te pakken. Waarom en hoe lees je in dit artikel.
Kinderen leren al jong dat ze via tellen kunnen bepalen hoeveel voorwerpen of afbeeldingen ze zien. Na enige tijd komen ze erachter dat er ook optellen en aftrekken bestaat. Dat blijkt een handige oplossing te zijn om veel tellen overbodig te maken. Als het goed is ontdekken ze dan ook dat optellen en aftrekken elkaars omkering zijn: je spoelt als het ware het filmpje weer terug. Dat is een uiterst waardevolle ontdekking, want zo blijken drie getallen op vier manieren met elkaar gecombineerd te kunnen worden: 5+3=8; 3+5=8; 8-3=5; 8-5=3.
Nog weer wat later blijken er nog twee bewerkingen te zijn die een tijdrovende situatie kunnen oplossen: vermenigvuldigen en delen maken veel van hetzelfde optellen of aftrekken overbodig. Zo bouwen ze voort op hun voorkennis en merken dat rekenen vol handige oplossingen en onderlinge verbanden zit…
Het begint met ervaren
De introductie van vermenigvuldigen en delen gebeurt, net als optellen en aftrekken, door de kinderen handelend bezig te laten zijn. Ook hierbij komen direct beide bewerkingen aan de orde, want ook die zijn elkaars omgekeerde. Dit is niet vreemd voor wie al eerder heeft ervaren dat dit bij optellen en aftrekken ook zo is en vervolgens herkent dat vermenigvuldigen en delen eigenlijk bijzondere vormen van optellen en aftrekken zijn.
De eerste situatie waarin ze vermenigvuldigen tegenkomen is het herkennen van een verzameling groepjes. Dat kunnen de paren schoenen (of voeten) zijn die in de kring op de grond staan, maar ook doosjes met potloden, zakjes met stroopwafels of kisten met blokken. Als je goed rondkijkt, op school, thuis of in een winkel, ga je overal zulke gelijke groepjes zien, als je erop let. De vraag die daar dan bij hoort is: hoeveel dingen zijn dat bij elkaar?
Neem die schoenen in de kring. Ze kunnen die al vroeg met sprongetjes van twee tellen: 2 – 4 – 6 - … . In feite zijn ze dan al aan het herhaald optellen: 2+2+2+2+… Als er 24 kinderen met hun leraar in de kring zitten, zijn er dus 25 keer 2 schoenen en dat blijken er dan vijftig te zijn.
Maar als je weet dat er vijftig schoenen in de kring staan, en je weet dat ieder er twee aan heeft, dan kun je ook te weten komen hoeveel mensen er in de kring zitten. Dan moet je die vijftig delen door twee, of steeds er twee aftrekken en bijhouden hoe vaak je dat doet.
Dit type situaties, waarin groepjes samengevoegd worden of waarin van een grotere hoeveelheid groepjes gevormd worden, is een van de drie contexten waarin vermenigvuldigen en delen samen voorkomen.
Het zijn beide situaties die kinderen vaak kunnen tegenkomen en waarin deze bewerkingen dus als een handige aanpak kunnen worden toegepast. Door de kinderen dit in drietallen te laten herkennen en uitproberen ontwikkelen ze mentale beelden van wat een vermenigvuldig- of deelsituatie is en wat daarvan het essentiële kenmerk is. Het gaat dan namelijk steeds om evengrote groepjes. Zijn de groepjes verschillend van aantal, dan blijft er niets anders over dan te blijven optellen of aftrekken.
Het herkennen van patronen
Dan is het tijd om op het plein een tweede situatie te gaan ervaren. Daar liggen hoogstwaarschijnlijk vierkante tegels. Met stoepkrijt heb je een rechthoek van bv. 6 bij 8 tegels getekend, precies langs de randen van de tegels. Omdat die tegels waarschijnlijk ‘in verband’ liggen moet je even afspreken dat twee halve tegels gewoon als één tegel tellen. Twee leerlingen mogen meehelpen, de anderen staan er in een ruime kring omheen. Leerling A gaat voor het midden van een lange zijde staan, leerling B voor de korte zijde. Om beurten mogen ze vertellen hoeveel rijen (dus tegels in een voor hen horizontale rij) zij voor zich zien.
De anderen moeten zich proberen voor te stellen wat die twee zien. Dan blijkt de een 6 rijen van 8 tegels te zien en de ander 8 rijen van 6. Ze zien allebei precies dezelfde tegels, alleen vanuit een ander perspectief. Optellend komen ze er samen wel achter dat het er 48 zijn. Dat roept dan de vraag op: als ik met 48 tegels rijtjes van 8 ga leggen, hoeveel rijtjes kan ik dan maken? Precies diezelfde situatie illustreert zo dat vermenigvuldigen en delen elkaars omgekeerde zijn.
.jpg)
Daarna mogen de anderen op andere plekken op het plein ook een rechthoek afbakenen en proberen of het daar ook zo gaat. Nadat ze daarvan in de kring kort verslag hebben gedaan trek je met hen de conclusie dat 6x8=48, maar 8x6 natuurlijk ook. En dat 48:8=6 en 48:6=8 ook bij diezelfde tegels passen. Je mag dus blijkbaar die twee getallen verwisselen, zonder dat de hoeveelheid anders wordt. Het verschil komt doordat je vanaf een andere zijkant ernaar kijkt.
Deze context komt ook vaak voor, zoals deze foto illustreert. Heel veel gebouwen hebben de ramen in keurige rijen geordend. De glazenwasser die een begroting moet maken zal hier niet gaan optellen. Ook koeken of kruidnootjes op een bakplaat laten zo’n patroon zien. Ook de bakker telt die rijen niet op en bij het vullen van zakjes daarmee trekt hij ook niet herhaald af. Volop gelegenheid om de kinderen die week de kans te geven minstens twee foto’s te maken van zo’n situatie. Die foto’s hangen ze geprint op een prikbord of slaan ze digitaal op via het digibord. Ze kunnen daarna in duo’s bij elke foto bedenken welke vier sommen bij elk van die situaties passen.

Het gaat er in deze fase nog steeds vooral om te leren herkennen in welke situaties vermenigvuldigen en delen aan de orde zijn en het optellen en aftrekken vervangen.
De bewerking als vervolgverhaal
De derde context waarbinnen kinderen vermenigvuldigen en delen kunnen herkennen is de lijn, waarop gelijke delen elkaar opvolgen. Een simpel voorbeeld is de avondvierdaagse, waarop kinderen op vier opeenvolgende dagen 5 of 10 km lopen. Na die vier dagen hebben ze dus 4 x 5 km of 4 x 10 km gelopen.
Een ander herkenbaar voorbeeld is de fiets. Al fietsend draait het voorwiel rond en begint steeds weer opnieuw aan het volgende stuk. Als je de omtrek van dat wiel weet en je houdt bij hoe vaak dat wiel ronddraait, dan kun je de lengte van die route uitrekenen.
Omgekeerd kun je, als weet hoe ver het is van huis naar school, uitrekenen hoe vaak je wiel dan is rondgedraaid. Opnieuw wordt dan weer duidelijk dat vermenigvuldigen en delen in dezelfde context steeds over dezelfde getallen gaan en elkaars omgekeerde zijn.

Die lijncontext kun je ook herkennen in muziek. De opeenvolgende maten op de notenbalken tellen als basis een gelijk aantal dezelfde noten, zoals in een driekwartsmaat, waar in elke maat drie kwartnoten staan (ook al kunnen die soms zijn onderverdeeld in achtsten of samengevoegd tot een halve. Al die opeenvolgende maten vormen een compositie, met een bepaalde maatsoort en een lengte die voortkomt uit het aantal gebruikte maten.

Dit soort inzichten moet steeds zijn gebaseerd op eigen ervaring en niet slechts op een demonstratie.
Dit is nodig om ervoor te zorgen dat de essenties in het brein goed wordt opgeslagen.
Het feit dat je de getallen uit die vermenigvuldiging mag verwisselen is geen trucje, net zomin als de koppeling van vermenigvuldigen en delen een trucje is. Deze ervaringen leiden tot begrip en kennis, maar die zijn niet te vervangen door instructie, doordat dit dan al snel beperkt blijft tot kale weetjes, die eerst vooral een beroep doen op het werkgeheugen. Zonder verbindingen vanuit de eigen voorkennis en de herkenning vanuit eerdere ervaringen en daar gevormde mentale beelden, is dat heel kwetsbaar en meestal tijdelijk.
Wel is het nuttig om die ervaringen te inventariseren en op basis daarvan zo nodig nog wat accenten aan te geven. Dit moet Dan wel pas nadat de kinderen hun ontdekkingen in kleine groepjes hebben kunnen verwoorden. Pas dan kunnen die accenten uit de nabespreking goed landen. De kinderen moeten daarvoor eerst nieuwe mentale beelden hebben opgebouwd en hun betekenis hebben kunnen verwoorden..
De achterliggende systematiek
Als de kinderen zover zijn, komt het moment dat de systematiek achter de sommen verkend kan worden. Om dat te kunnen beginnen moeten de betreffende leerlingen het optellen en aftrekken tot 100 vlot kunnen uitvoeren. Wie nog niet zover is, moet zich dat eerst eigen maken, want dit blijkt essentiële voorkennis om gebruik te kunnen maken van al bekende sommen als tussenstap, zoals bij 9 x7. Daar is 10 x 7 de hulpsom, omdat je daarvan dan 1 x 7 kunt aftrekken. Daartoe moet je wel vlot 70 – 7 kunnen uitrekenen.
Traditioneel zou je dit moment de introductie van de ‘tafels’ hebben genoemd. Het begrip tafel is echter te vergelijken met ons begrip ‘poster’, een groot bord waarop een tekst tentoongesteld wordt. In dit geval zou dat een rijtje sommen zijn. Die gewoonte stamt nog uit een tijd dat klassikaal lesgeven en rijtjes uit het hoofd laten leren nog zinvol werden geacht.
Het introduceren van de sommen vraagt echter veel meer actie van de leerlingen zelf. Alleen zo krijgen zij actief zicht op de samenhang en de dwarsverbanden. Bovendien heb je aan het kunnen opzeggen van die hele rij in de praktijk niets, omdat je altijd losse sommen nodig hebt. Dan ga je niet eerst zo’n rij opzeggen, net zomin als je in Duitsland de rij voorzetsels van de 3e of 4e naamval gaat opzeggen als je Duits spreekt en zo’n voorzetsel wilt gebruiken.
Het gaat er daarom nu om dat de leerlingen het systeem van de tabellen met vermenigvuldigingen en delingen gaan doorzien en gebruiken. Daarvoor heb je lege tabellen gemaakt die ze in kleine groepjes straks verder gaan invullen.
Natuurlijk maak je ook nu gebruik van de combinatie vermenigvuldigen en delen. Dat is niet alleen omdat beide bewerkingen bijelkaar horen, maar ook omdat dit straks veel leerwinst oplevert. Het gaat ook hier immers steeds om dezelfde drie getallen die in vier variaties voorkomen.
Om de kinderen een beeld te geven van wat de bedoeling is, doe je de tabellen van 1 voor. Je geeft wel steeds even bedenktijd voor je het volgende getallentrio invult. Het gaat er immers om dat de leerlingen de systematiek door hebben. Zo komen steeds twee sommen naast elkaar te staan, bv. 3 x 1 = 3 | 3 : 1 = 3.
Nadat deze twee rijen compleet zijn stel je de vraag welke sommen uit de tabellen van 2 t/m 10 je nu ook al weet. Dat zijn inderdaad dezelfde combinaties, maar dan in omgekeerde volgorde. In het voorbeeld hiervoor wordt dat dus 1 x 3 = 3 en 3 : 3 = 1. Daarmee heb je niet alleen steeds het kwartet met deze trio’s compleet, maar heb je van alle nog resterende tabellen al een som ingevuld.
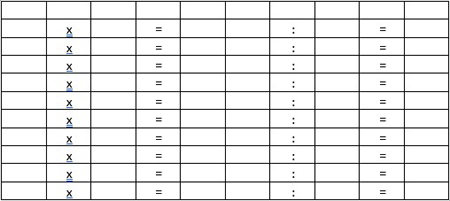
Nu krijgen de leerlingen, in groepjes van drie, de opdracht om samen de twee tabellen van 2 in te vullen. De uitdaging die je meegeeft is om dat niet op volgorde te doen en dus steeds 2 erbij te doen, maar samen te zoeken naar handiger manieren waarbij je de tabel niet op volgorde invult. Dat kan door verdubbelen, waardoor je van 2x naar 4x en 8x springt. Daar komen ze natuurlijk samen wel uit, maar het nagesprek moet dan vooral gaan over de manier waarop ze die getallen hebben gevonden en hoe ze vermenigvuldigen en delen hebben verbonden. Sommigen zullen verticaal gewerkt hebben en eerst alle vermenigvuldigingen ingevuld. Anderen hebben juist steeds horizontaal gewerkt en direct gebruik gemaakt van hetzelfde trio getallen. Laat ieder bedenken wat de voordelen van elke aanpak zijn.
Als de tabellen van 2 klaar zijn en besproken komt deze vraag weer terug: wat weet je nu ook van de andere acht tabellen? Dat zal voor de meesten nu geen verrassing meer zijn: alle 2x…=… en …:…=2 varianten kunnen ze nu zo invullen.
Beelden ontwikkelen
Daarna laat je hen even bespreken welke tabel ze hierna willen invullen. Daarbij moeten ze proberen te bedenken hoe ze de al ingevulde tabellen daarbij zouden kunnen benutten. Sommigen zullen dan de tabel van 4 kiezen, omdat dit tweemaal zoveel is als die van 2. Anderen doen die van drie, omdat ze herkennen dat 3x hetzelfde is als 1x en 2x samen, of omdat dit gewoon de volgende tabel is… Ook die van 10 kan als heel eenvoudig worden herkend.
Steeds als zo’n tabel af is, vullen ze die trio’s op de juiste manier in bij de nog overgebleven tabellen. Zo maken ze de rest van de tabellen verder af en merken dat er dan steeds minder lege plekken over zijn gebleven. Wat in elke tabel altijd openblijft zijn de sommen als 6 x 6 = .. en .. : 6 = 6. Laat hen zelf bedenken waardoor dit komt en voorspellen welke plek in de tabel van 9 straks openblijft. Het gaat inderdaad om de sommen die in geen van de andere tabellen voorkomen, doordat (bij vermenigvuldigen) de beide getallen links van de = gelijk zijn of (bij delen) doordat de beide getallen rondom de = gelijk zijn. Het is prima om in dit verband het woord ‘kwadraat’ te gebruiken, maar wel zo dat de kinderen het eerder als een ‘bonus’ ervaren , dan als een eis.

Het kan in deze fase helpend zijn om die structuur van al die vermenigvuldigingen en delingen voor je te zien. Dat kunnen kinderen zelf maken. Vooraf moeten ze bedenken hoeveel voorwerpen of stippen je maximaal nodig hebt om die tien tabellen neer te leggen of te tekenen. Dat wordt inderdaad bepaald door de laatste som: 10 x 10 = 100. Door van boetseermateriaal honderd balletjes te vormen en die in rijtjes van tien te ordenen, kun je met twee slierten van dat materiaal de betreffende som afbakenen, zoals op de foto.
Het aardige van dit soort schematische voorstellingen is dat ook de andere sommen uit die tabel zo herkenbaar zijn, zowel die eerder, als die later in de tabel voorkomen
Dit geldt ook voor hetzelfde aantal groepjes, maar dan in eerdere of volgende tabellen. In feite beeld je zo de verhouding met wat eerder pof later komt uit. Dat is een sterke steun bij het grip krijgen op de inhoud van deze tabellen.
Oefenen met uitrekenen
Als alle tabellen zijn gevuld en de kinderen onder woorden kunnen brengen hoe de diverse sommen met elkaar verbonden zijn, binnen dezelfde tabel en tussen verschillende tabellen, komt de volgende stap.
Ze werken weer in drietallen en mogen om beurten elkaar een som noemen. De andere twee moeten die dan uitrekenen en daarna elkaar vertellen hoe ze dat hebben gedaan. De uitdaging daarbij is om dit zo slim mogelijk te doen. Dat kan door verdubbelen of halveren, maar ook door al bekende sommen te gebruiken en die op te tellen of af te trekken, zoals 5x te vinden door 2x en 3x op te tellen of door 10x te halveren.
Zodra ze door beginnen te krijgen hoe ze handig te werk kunnen gaan, kunnen ze in hun groepje afspreken welke tabellen ze eerst willen oefenen, zodat het uitrekenen daarvan helemaal vlot gaat. Dit oefenen van het uitrekenen langs een zo kort mogelijke route heet automatiseren. Er is dan dus altijd sprake van uitrekenen en niet van weten. Het is mogelijk dat dit uitrekenen bij sommige sommen al vlot gaat, maar bij andere nog wat meer moeite kost. Die laatste soort kunnen ze dan op kaartjes schrijven en die de volgende keer extra oefenen en bespreken. Op die kaartjes komen dan twee sommen: de deelvariant en op de achterkant de vermenigvuldigvariant. Het is de bedoeling dat ze steeds de vermenigvuldigsom en de bijbehorende deelsom uitrekenen. Het is aan te bevelen die beide bewerkingen regelmatig af te wisselen. Zo zullen ze de ene keer met de deelsom starten en een andere keer met de vermenigvuldigsom beginnen, maar ze steeds wel beide doen.
Ongetwijfeld ontdekken ze dat er sommen zijn die ze al compleet weten en niet meer hoeven uit te rekenen. Dat zullen eerst de 1x, 2x en 10x series zijn, maar al gauw zijn er ook al een paar uit andere tabellen bij, want als ze zich realiseren dat elk trio bij een kwartet hoort, weet je zo al direct vier varianten.
Oefenen met weten
Dan wordt het tijd om toe te werken naar het verder memoriseren van die tweehonderd sommetjes. Dan mag je niet meer uitrekenen, maar gaat het om feitenkennis. Dat oefen je als volgt. Alle sommen (x en :) staat op aparte kaartjes, compleet met antwoord. Dat laatste is het verschil met automatiseren, waar het nog gaat om uitrekenen.
Bij memoriseren gaat het om het auditief en/of visueel inprenten van het trio getallen, dus inclusief het antwoord.
Dit oefenen kinderen in tweetallen. De een laat het kaartje heel kort zien en de ander zegt de som die daar stond. Direct daar achteraan noemt die leerling ook de drie andere sommen van het kwartet dat bij die drie getallen hoort. De andere leerling controleert of de juiste getallen worden genoemd. Als dat in orde is, komt het volgende kaartje. Het is aan de leerlingen om te kiezen of ze om beurten een kaartje pakken, of dat ze eerst bv. tien kaartjes door de een laten pakken en pas daarna wisselen.
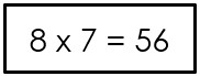
In het begin zullen ze beiden nog ongeveer dezelfde sommen willen oefenen. Komen ze wat verder dan kan er verschil ontstaan en zal een eigen serie nog te oefenen kaartjes hebben. Dat kan door ieder twee doosjes te geven: een voor de gekende trio’s en een voor de nog te oefenen trio’s.
Het is dan wel aan te bevelen af en toe te laten checken of die ‘gekende’ sommen nog steeds gekend zijn. Dat blijkt dan met name doordat ze de andere drie van het kwartet vlot kunnen noemen. Als variant kunnen ze ook alleen de som op het kaartje voorlezen, waarna de ander die herhaalt en de andere drie er achteraan zegt.
Om deze kennis te toetsen kunnen kinderen elkaar sommen geven, waarin een van de drie getallen ontbreekt. Dat hoeft dus niet steeds het getal na het isgelijkteken te zijn.
Let op: dit is dus niet een oefenaanpak, maar een vorm van formatief toetsen. Zo kunnen leerlingen zelf nagaan in hoeverre die trio’s als vaste combinatie van drie getallen al feitenkennis zijn geworden. De trio’s die nog niet genoeg gekend zijn, moeten dus vaker worden geoefend op de hiervoor beschreven manieren.
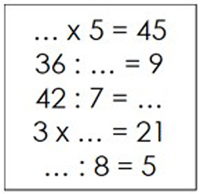
Toepassing van deze kennis
Zodra de tabellen t/m 10 bekend zijn, kunnen leerlingen die gaan toepassen bij wat grotere getallen. Een som als 15 x 7 kan dan worden herkend als de combinatie van 10 x 7 en 5 x 7, maar ook als de helft van 30 x 7. Met nog wat grotere getallen gaat dit ook zo: 24 x 568 kan dan via 2 x 568 verder worden opgelost. 2 x 568= 1000+136= 1136, zodat 20 x 568 11360 is en 4 x 568 het dubbele is van 1136.
Dit is niet bedoeld om beter te worden dan een rekenmachientje, maar wel om te leren herkennen hoe je je voorkennis kunt benutten. In de praktijk buiten de rekenles zullen leerlingen dit soort sommen op hun smartphone uitrekenen als een precies antwoord nodig is.
Vaak is dit niet nodig, waardoor het kunnen schatten veel belangrijker is. Dit is daarom eerder nuttige oefenstof dan het veel oefenen met vermenigvuldigen onder elkaar. Dit vraagt weer om samenwerking in kleine groepjes, zodat leerlingen samen bedenken hoe je handig kunt afronden bij verschillende getallen. Wat handig is hangt af van de context (waarvoor heb je een antwoord nodig?), van de getallen en van je voorkennis.
Bij veel prijzen is het afronden niet zo ingewikkeld. Wie 16 x € 5,99 wil uitrekenen, maakt daarvan natuurlijk 16 x € 6,00 en dat is dan niet ingewikkeld meer. Bij het voorbeeld hierboven (24 x 568) zou 24 x 600 een mogelijkheid zijn, maar ook 25 x 468, door dat te transformeren naar 25 x 4 x 117. Dit lukt alleen als je herkent dat 4 x 25 = 100 en dat 468 door vier te delen is.
Bij een som als 376 : 4 is afronding naar 400 : 4 voor elke leerling wel haalbaar. Dan blijft de vraag of het verschil moet worden gecorrigeerd. In dit geval zou dat niet moeilijk zijn, doordat 24 : 4 precies 6 oplevert, waardoor 100 – 6 tot het precieze antwoord leidt. Dit soort toepassingen, het liefst aan de hand van concrete contexten, als reclamefolders, actualiteiten of onderwerpen uit de wereldoriëntatie vragen om mondeling oefenen en kritisch in dat oefengroepje bespreken. Niet het antwoord is dan bepalend, maar de argumenten voor een gekozen aanpak. Daarmee brengen ze elkaar op ideeën, leren ze kritisch én creatief denken en herkennen ze het nut van zulk rekenwerk.
Het traject in vogelvlucht
Zo voldoet de introductie van en het thuisraken in vermenigvuldigen en delen aan de belangrijkste eisen die eigentijds rekenwiskundeonderwijs effectief maken.
De start is gericht op herkennen en ervaren, waarbij tevens wordt aangesloten bij de al aanwezige voorkennis en er perspectief wordt geboden op de toepassing in het dagelijks leven buiten de rekenles.
Vervolgens zijn de leerlingen zelf actief en werken daarin samen met anderen, zodat ze hun keuzes en ontdekkingen moeten verwoorden en delen. De keuze voor het werken in groepjes van drie in plaats van met een tweetal is om te voorkomen dat de een steeds bepaalt en de ander volgt.
Het herkennen en benutten van de samenhang tussen beide bewerkingen en tussen de verschillende tabellen zorgt niet alleen voor meer inzicht, maar levert in het traject daarna veel tijdwinst op.
Daarna volgt het eigen maken van de uitrekenprocedures en die zoveel mogelijk verkorten, wat bekend staat als automatiseren. Dit gebeurt mondeling en op maat, doordat de leerlingen zelf de trio’s kiezen die nog geoefend moeten worden. Dit legt qua aanpak de basis voor het latere rekenen met wat grotere getallen.
Daarna volgt het verder verwerven van de feitenkennis, waardoor zij de kwartetten met trio’s zonder rekenen kunnen noemen. Dit staat bekend als memoriseren, een essentieel verschil met automatiseren, ook qua aanpak. Ook dat gebeurt mondeling en op maat.
Tenslotte wordent al deze kennis en inzichten gebruikt om die verder toe te passen met wat grotere getallen uit concrete en voor hen betekenisvolle contexten.