Zie je het voor je? Rekenen is per definitie talig!
Dolf Janson
Senior onderwijsadviseur en -ontwikkelaar bij Jansonadvies
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/rekenen-taal-voorstelling-betekenis.php

Voorstellen als aanjager voor leren rekenen en de relatie tussen taal en beeld daarbij.
Rekenen op taal
Rekenonderwijs is per definitie talig. Je hebt woorden nodig om over getallen en hun betekenis te kunnen communiceren. Bovendien krijgen getallen buiten de rekenles altijd hun betekenis binnen een bepaalde context. Zo’n context gaat gepaard met specifieke woorden en betekenissen. Het gebruik van die woorden roept daardoor beelden op, die helpen om je te kunnen voorstellen wat er gebeurt, wat de relatie tussen de getallen is en wat van de gebruiker (de rekenaar) gevraagd wordt.
Uit diverse onderzoeken is gebleken dat leerlingen die niet in staat zijn woorden en beelden (voorstellingen of representaties) te verbinden en/of op te roepen, minder profijt hebben van hun (reken)onderwijs. Zij groeien uit tot minder goede rekenaars. Dit is niet het gevolg van minder aanleg, maar van ontoereikend onderwijs.
Woorden en betekenissen
Leerlingen brengen een bepaalde woordenschat mee als ze op school komen. Dat zijn woorden uit de dagelijkse taal, zoals ze die thuis en in hun omgeving hebben opgepikt. Een deel van die taal kan bestaan uit specifieke betekenissen, die men thuis of in de buurt aan bepaalde woorden geeft. Op school komt daar de schooltaal bij: allerlei woorden die hun betekenis ontlenen aan de schoolcontext. Daarnaast maken de leerlingen (hopelijk niet voor het eerst) kennis met de meer formele taal zoals die in geschreven teksten voorkomt: voorlezen opent werelden met complete zinnen en nieuwe woorden en/ of andere betekenissen. Prentenboeken, illustraties, filmpjes en digitale spelletjes vullen dat aan met beelden, waardoor zij woorden, betekenissen en visualiseringen daarvan kunnen verbinden.
"Elke leerling geeft zijn eigen betekenis aan woorden."
Ervaren vormt beelden
Meer specifiek voor rekenwiskundeactiviteiten geldt dat ervaringen en het zelf hanteren van allerlei materialen een noodzakelijke basis vormen voor ruimtelijk inzicht en het onthouden en verbinden van begrippen en betekenissen. Het doen, ervaren, zien en verwoorden leiden ertoe dat er verbindingen in het brein ontstaan die de basis vormen voor verdere leerprocessen. Het is hierbij niet of-of, maar en-en: zelf doen en ervaren, zien wat er gebeurt en hoe dingen er uitzien en dat alles onder woorden brengen en daarover communiceren, zodat je ook weer reacties (feedback) terugkrijgt, horen bij elkaar. In het zogenaamde Handelingsmodel, de gestructureerde uitwerking van de ‘ijsberg’, staan deze aspecten als fasen geordend.
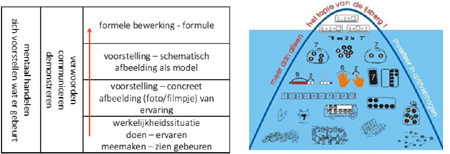
Voorkennis is uitgangspunt
Bij elk rekenthema en daardoor in elke rekenles is het steeds weer nodig na te gaan welke woorden en welke betekenissen van woorden essentieel zijn om te kunnen leren daarmee. Het is dan nodig je als leraar te realiseren wat het voor leerlingen betekent als zij aan zulke begrippen betekenis moeten geven en daarmee verder denken. Het oproepen van beelden, zowel heel concrete (hoe ziet dat eruit?) als meer schematische (wat zijn de essentiële gegevens?) is daartoe noodzakelijk. Valkuilen hierbij zijn veronderstellen dat de leerlingen dat al wel zullen weten, of niet alert zijn op mogelijk andere betekenissen of connotaties die leerlingen kennen bij gebruikte woorden.
Voorbeeld: Hij heeft 5 kleurtjes meer dan zijn maatje. Zij heeft geen kleurtjes meer. Als hij 5 kleurtjes meer had gehad, hadden hij en zijn maatje er evenveel.
Deze twee woorden ‘kleurtjes meer’ hebben in elke zin een (iets) andere betekenis. Juist zulke betekenisnuances kunnen leiden tot een verkeerd interpreteren van de situatie. De beschrijving roept dan andere beelden op van wat er gebeurt en dat leidt dan ook tot andere berekeningen.
Bij rekenopgaven kan er sprake zijn van verschillende situaties:
- een verandering: een hoeveelheid, een maat of een verhouding verandert door een gebeurtenis;
- een vergelijking tussen twee of meer hoeveelheden, maten of verhoudingen, waarbij deze hoeveelheden niet altijd direct gegeven zijn.
In beide gevallen helpt het als de leerlingen uit (de beschrijving van) de situatie kunnen afleiden wat er aan de hand is en wat van hen wordt gevraagd èn als zij zich een voorstelling kunnen maken van hoe dat er uitziet. Met name het systematisch analyseren en schematisch weergeven van zo’n opgave is zeer helpend om de juiste stappen te kunnen zetten en de goede conclusies te kunnen trekken. Hierbij is het verwoorden en kritisch nagaan of de (mentale) beelden kloppen nodig om verder te komen.
Samenwerken met een maatje en coachingsgesprekjes in kleine groepjes zijn hierbij een belangrijke voorwaarde voor succes. Het is namelijk noodzaak dat een leerling zelf begrijpt hoe visualisering kan helpen en in staat is de gegevens daarvoor uit de opdracht af te leiden. Trucjes, voorkauwen of toepraten naar het antwoord tijdens verlengde instructie of herhaald maken van veel gelijkvormige opgaven leiden niet tot het gewenste leer effect, zeker niet voor de wat langere termijn. De leerling moet zelf actief en doelbewust daarmee kunnen oefenen.
Het strookmodel
Een van de manieren waarop leerlingen kunnen leren om rekensituaties visueel te maken is het gebruik van het strookmodel. Dit model komt voort uit de zg. Singapore-aanpak (Ban Har Yeap, 2011). Het strookmodel visualiseert drie situaties:
- verschil tussen voor en na een handeling of gebeurtenis;
- de relatie tussen een deel en het geheel;
- een vergelijking van twee of meer naast elkaar voorkomende situaties.
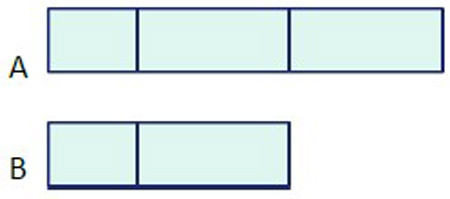
Door het gebruik van stroken gelijk te laten meelopen met de voortgang door de domeinen van rekenen, leren leerlingen steeds handiger met dit model omgaan. Voorwaarde is wel dat er steeds aandacht is voor het beeld dat een opgave oproept, het zelf adequaat leren verwoorden daarvan en het daarna schematisch weergeven. Die weergave moet een leerling ook weer zelf kunnen verklaren.
Het gaat in veel gevallen niet om een standaardweergave, maar om een weergave van de eigen interpretatie en/of associatie. Die kan verschillend zijn bij verschillende leerlingen, doordat o.a. de eigen voorkennis hierbij een rol speelt. Dat is prima, mits zij elkaar maar (kunnen) uitleggen welke kenmerken tot hun weergave hebben geleid. Daarmee achterhaal je als leraar eventueel verkeerde interpretaties. Ook blijkt hieruit welke kennis zij gebruiken bij het oplossen. Dit kan dan aanleiding zijn om met bepaalde leerlingen in gesprek te gaan om hen tot verdieping of verdere ontwikkeling uit te dagen.
Zorg er wel voor dat je zelf eraan went om mentale en concrete voorstellingen in je lessen te integreren.
"Ruim altijd tijd in voor werkvormen waarin het verwoorden van mentale en concrete voorstellingen functioneel is."
Lastige opgaven
Uit onderzoeken blijkt dat de formulering van opgaven een bron van verwarring kan zijn. Veel opgaven zijn gebaseerd op het vergelijken van twee situaties, die of uit elkaar voortvloeien (bv. korting) of naast elkaar bestaan. Wanneer het verschil kan worden bepaald door iets toe te voegen aan de een en de beschrijving van die situatie gebruikt woorden als meer of erbij, dan spreken we van een consistent probleem. Gebruikt men in zo’n vergelijking waarin iets meer wordt juist woorden als minder of over, dan noemen we dat een inconsistent probleem.
Vergelijk de volgende opgaven op dit punt! Welke is inconsistent?
Bij AH kost een fles vers sap € 4,00.
Dat is € 2,00 minder dan bij De Spar.
Hoeveel moet ik bij De Spar betalen voor 3 flessen vers sap?
Bij AH kost een fles vers sap € 4,00.
Bij De Spar kost zo’n fles € 2,00 meer.
Hoeveel moet ik bij De Spar betalen voor 3 flessen vers sap?
Dit probleem is te voorkomen of tenminste te verminderen door leerlingen eraan te wennen een probleem met eigen woorden te beschrijven en dan zich zo’n situatie voor te stellen. Dat kan bijvoorbeeld op de manier van ‘Solve it!’:
- Lees de tekst.
- Vertel het met je eigen woorden na.
- Maak een voorstelling van het probleem: hoe ziet het eruit? (Op papier of in gedachten)
- Bedenk een plan om het op te lossen.
- Reken het uit.
- Controleer of je antwoord klopt met de tekst.
Je mag als je wilt erbij tekenen
Het is hier en daar gebruikelijk dat leerlingen, als ze hun opdracht afhebben, die bladzijde mogen illustreren met een bijpassende tekening. Dat komt zeker bij het schrijven van eigen teksten regelmatig voor. Die wat vrijblijvend geformuleerde opdracht klinkt dan als de titel hierboven.
Bij leren rekenen is het maken van een tekening geen beloning voor wie klaar is, noch een vorm van versiering. Het maken van een tekening is in de rekenles heel functioneel. Het helpt leerlingen om kritisch de opdracht te lezen, te analyseren en de gegevens te ordenen. Dit maakt het de leerling beter mogelijk om de juiste bewerkingen te kiezen en ook om het zo verkregen antwoord te interpreteren.
Een tekening, ook in de vorm van een simpel weergegeven schema, helpt vooraf, tijdens en na de uitvoering. Met name de mogelijkheid om terug te kijken en na te gaan of de juiste stappen zijn gekozen en de correcte conclusie getrokken, maakt het weergeven van de opgave in een modelmatige voorstelling waardevol.
Als leerlingen net kennismaken met het tekenen van iets dat ze hebben ervaren of echt gezien of vastgehad, is het echt tekenen van die situatie een prima tussenstap. Dan mogen ze de hele rij huizen tekenen om te laten zien hoeveel huizen er tussen nummer 5 en nummer 13 staan. Later leren ze dat ze kunnen volstaan met vierkantjes of met het tekenen van twee stroken.
In plaats van die ’echte’ tekening kan een foto met een (oude) telefoon ook volstaan. Dat kost minder tijd en kan door twee leerlingen samen besproken worden, waardoor de noodzakelijke communicatie nog meer wordt uitgelokt. Uiteindelijk gaat het erom dat leerlingen leren een situatie schematisch weer te geven. Daartoe hoeft het niet eens precies naar verhouding uitgemeten. De onderlinge ordening is de kern.
Ogen dicht…
Om te stimuleren dat leerlingen zich beelden vormen, kan het helpen om tijdens het (dagelijkse!) voorlezen af en toe de opdracht te geven hun ogen dicht te doen. Daardoor lukt het hen nog beter om een verhaal als een film voor zich te zien. In de nabespreking zal blijken dat niet iedereen hetzelfde zag. Ook dat is een nuttige ervaring, want daarmee kan duidelijk worden wat het verschil is tus-sen de hoofdzaken en de details. Als het gaat om een rij van 8 bomen, zal de een beuken en een ander appelbomen voor zich zien. In een rekenopgave is zo’n verschil geen probleem. In een verhaal draagt het bij aan ieders persoonlijke beleving van de sfeer.