Het effect van gericht automatiseren van rekenvaardigheden
Marjolein Zwik
Leerkracht basisonderwijs en Master SEN bij Unicoz onderwijsgroep
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/rekenen-automatiseren.php

Samenvatting
De laatste jaren is er veel maatschappelijke en politieke aandacht voor het verbeteren van de basisvaardigheden van het rekenen. Deze vaardigheden zijn onmisbaar voor het verdere verloop van de schoolloopbaan van onze leerlingen. Het automatiseren (Kerndoel 27 van het basisonderwijs) wordt als één van de tekortkomingen genoemd in de huidige realistische rekenmethodes (Van de Craats, 2007; Gelderblom, 2007 en 2008; Ruijssenaars, Van Luit en Van Lieshout, 2004).
In dit praktijkonderzoek doe ik verslag van mijn bevindingen naar aanleiding van een interventie, gericht op het verbeteren van het automatiseren van basisbewerkingen van het rekenen tot honderd in een groep 5. Mijn hoofdonderzoeksvraag luidt:
• Wat is het effect van een dagelijkse oefensessie gericht op het automatiseren van de basisvaardigheden van het aanvankelijk rekenen (optellen en aftrekken tot 20 en optellen en aftrekken tot 100)?
Mijn interventie is gericht op de optel- en aftreksommen tot honderd met en zonder overschrijding van een tiental. Hierbij is o.a. gebruik gemaakt van coöperatieve didactische werkvormen volgens Kagan (2004).
Ik heb gebruik gemaakt van een experiment (Verschuren en Doorewaard, 2004), dat wil zeggen dat de effecten van de interventie in een experimentele groep worden vergeleken met de resultaten van een vergelijkbare controlegroep, middels een nulmeting en een nameting. Tot slot heb ik de leerlingen van de experimentele groep hun competentiegevoel bij het rekenen laten evalueren aan de hand van een vragenlijst en een top 10 van favoriete werkvormen laten rangordenen.
Geconcludeerd kan worden dat de tijdens het experiment gebruikte oefenvormen in combinatie met coöperatieve werkvormen (Kagan, 2004), een gunstig effect hebben op het automatiseren van basisbewerkingen van optel- en aftreksommen tot honderd.
De leerlingen ervaren de werkvormen positief en zijn gemotiveerd en 68% heeft duidelijk het gevoel dat ze sneller kunnen rekenen na de interventie.
Achtergronden bij het automatiseren basisbewerkingen rekenen
Onder automatiseren wordt hier verstaan het vrijwel routinematig uitvoeren van rekenhandelingen. Als leerlingen de basisbewerkingen hebben geautomatiseerd, hoeven zij hun werkgeheugen minder te belasten bij het uitrekenen van complexere opgaven. Een groter deel van het geheugen blijft dan beschikbaar voor het uitvoeren van niet-geautomatiseerde rekenhandelingen.
Automatiseren is van belang voor het aanleren van vaardigheden die op een hoger cognitief niveau liggen (Ruijssenaars et al., 2004). Rekenzwakke leerlingen komen vaak moeilijk tot automatisering van basiskennis (Gelderblom, 2007 en 2008, Ruijssenaars et al., 2004). Hoewel automatismen niet voorwaardelijk zijn voor het leren rekenen is het wel van essentieel belang voor het vlot leren rekenen.
Automaticiteit houdt in dat het werkgeheugen ontlast wordt en het antwoord als rekenfeit uit het lange termijngeheugen wordt opgehaald. Volgens Ruijssenaars et al. (2004) is deze declaratieve kennis veel efficiënter dan de procedurele kennis, waarbij keer op keer procedurele fouten gemaakt kunnen worden en waarbij het werkgeheugen wordt belast. Dit is dan niet beschikbaar voor het uitvoeren van complexere rekenproblemen. Er ligt als het ware een hypotheek op de rekensnelheid.
Er zijn verschillende factoren te noemen die van invloed zijn op het automatiseren. Verschillende onderzoeken (Ashcraft, 1992, 1995 en Zbrodoff, 1996, geciteerd in Ruijssenaars et al., 2004) maken melding van het somgrootte-effect (problem size effect). Dit houdt in dat de optelsom minder makkelijk geautomatiseerd wordt naar mate het bijtelgetal toeneemt (3+2 is makkelijker dan 3+6, nog duidelijker wordt het bij 32+43).
Eén verklaring hiervan is dat sommen met kleine getallen vaker voorkomen in rekenmethoden en dus sneller herkend worden, het zogenaamde frequentie-effect. Een experiment van Zbrodoff (1996, geciteerd in Ruijssenaars et al., 2004) toont aan dat een combinatie van het frequentie-effect samen met interferentie (de mate waarin het onthouden van een som wordt verstoord door het proberen te onthouden van verwante sommen) het somgrootte-effect verklaren. Deze combinatie is voor kinderen de praktijk van alledag.
Hieruit vloeit voort dat er bij het automatiseren van feiten sprake is van associatie. Hierop is het Distributions of Associations model van Siegler (Ruijssenaars et al.,2004) gebaseerd. Heeft een kind een bepaalde som vaker gezien, zal de associatieve sterkte van het antwoord groter zijn en zal het antwoord eerder uit het lange termijngeheugen worden opgehaald.
Het geven van het antwoord hangt verder af van het zekerheidscriterium dat het kind inbouwt; is de druk om een goed antwoord te geven hoog, dan zal het kind eerder terugvallen op het toepassen van een strategie om het correcte antwoord te willen geven; dit kan zelfs een telstrategie zijn. Het nadeel van dit model is dat er bij een fout antwoord de verkeerde associatie ontstaat: een associatie van de som met het verkeerde antwoord.
In een herziening van het model (Adaptive Strategy Choice Model van Siegler en Shipley) (Ruijssenaars et al., 2004) wordt niet alleen een associatie gemaakt met het goede antwoord, maar tevens met de gebruikte, succesvolle strategie.
Geconcludeerd kan worden dat het niet alleen belangrijk is rekenkennis te automatiseren, maar ook om succesvolle rekenstrategieën aan te leren. In het model van Siegler is het essentieel dat er kan worden teruggevallen op een back-upstrategie. De didactiek van het automatiseren zou dus niet alleen op het inprenten (drill en practice) gericht moeten zijn, maar ook op het aanleren van effectieve rekenstrategieën (Braams en Denis, 2003 en Fuchs, 2006 en Ruijssenaars et al., 2004).
Interessant hierbij is dat onderzoek van Roussel et al. (2002) aantoont dat vermenigvuldigen en optellen makkelijker in het lange termijngeheugen worden opgeslagen dan aftrekopgaven. Bij aftrekopgaven wordt eerder gebruik gemaakt van een procedure en zijn er minder associatieve netwerken actief dan bij vermenigvuldigen en optellen. Een zelfde verschil is er aangetoond tussen optel- en aftrekopgaven, ten nadele van de aftrekopgaven (Thevenot en Barrouillet, 2006).
Bij optelopgaven zouden antwoorden zowel door het toepassen van rekenprocedures als door het ophalen van rekenfeiten uit het associatieve netwerk tot stand komen (Ruijssenaars et el., 2004). Het gebruiken van een procedure bij vermenigvuldigen is minder efficiënt dan inprenten en deze antwoorden worden voornamelijk opgehaald uit het lange termijn geheugen.
Mensen met problemen met het vermenigvuldigen vertonen ook vaker problemen met lezen en spellen (Ruijssenaars et al., 2004). Dit zou er mee te maken kunnen hebben dat woordbeelden ook voornamelijk uit het lange termijn geheugen opgehaald worden zonder tussenkomst van het werkgeheugen.
Onderzoeksopzet
Volgens Verschuren en Doorewaard (2004) zijn er verschillende onderzoeksstrategieën om een onderzoeksontwerp te maken. Ik heb gekozen voor een experiment, omdat dit hét type onderzoek is om ervaring op te doen met een nieuw gecreëerde situatie of proces en het effect na te gaan van deze verandering. Dit effect wordt duidelijk door twee gelijke groepen te maken volgens het ceteris paribus principe, waarbij de ene groep een interventie ondergaat en de andere groep niet. Het onderzoek is uitgevoerd in twee groepen 5 van nagenoeg dezelfde grootte op dezelfde school.
De effecten in de experimentele groep en de controlegroep worden bepaald door de verschillen tussen een voormeting en een eindmeting, respectievelijk begin januari 2011 en eind februari 2011 afgenomen. De interventieperiode bedroeg dus twee maanden. Voor zowel de nulmeting als de nameting is in beide groepen 5 gebruik gemaakt van de tempotoetsen van Maatwerk Oranje. Bij de nulmeting werden de instaptoetsen van onderdeel 2 en 3 afgenomen, bij de eindmeting werden de afsluitende toetsen van dezelfde onderdelen gebruikt.
De leerlingen zijn bij de evaluatie betrokken door middel van een enquête. Hierin kregen zij stellingen over hun competentiegevoel ten aanzien van het rekenen. Zij konden o.a. aangeven of zij vonden dat zij sneller zijn gaan rekenen door het trainingsprogramma. In de controlegroep is uitsluitend het reguliere rekenprogramma gevolgd.
De interventie
De interventie bestond uit korte, dagelijkse aandacht (5 à 10 minuten) voor automatisering met behulp van coöperatieve werkvormen en digitale werkvormen op het digitale schoolbord: Getallenlijn, twee dobbelstenen optellen, drie dobbelstenen optellen, Minsommen flitsen, plussommen flitsen, optellen met getallenkaartjes, plofsommen tot 100, splitsen, dobbelen met meerdere dobbelstenen, gooi met één, twee of drie dobbelstenen.
De structuren uit SCL (Kagan, 2004, Kole, De Hoop en Riemens, 2009) zijn:
• Binnen/Buitenkring
• Flitskaarten
• Genummerde Koppen Bij Elkaar
• Mix & Koppel
• Tweetal Coach
• TweeVergelijk
• Schud & Pak
De dagelijkse oefeningen vormden geen extra tijdsinvestering, maar werden binnen de reguliere rekentijd gepland. Dit om een zuivere vergelijking met de controlegroep te realiseren. Indien er extra rekentijd voor de interventie wordt ingepland kan het resultaat berusten op de extra tijdsinvestering. Bij de samenstelling en uitvoering van het interventieprogramma is gekozen voor oefenvormen die niet alleen een beroep doen op memoriseren (drill and practice), maar ook voor het gericht inoefenen van strategieën; oefenen onder het topje van de ijsberg (Moerlands en Van der Straaten, 2008).
De structuren van Structureel Coöperatief Leren (Kagan, 2004) lenen zich hier uitstekend voor, maar ook tijdens de digitale werkvormen is aandacht besteed aan proces en niet alleen aan het antwoord zelf.
De resultaten
De interventie
De resultaten van de tempotoetsen zijn weergegeven in afbeelding 1 en 2. Deze resultaten zijn gebaseerd op de groepsgemiddelden per toets, waarbij groep 5a de controlegroep en groep 5b de experimentele groep was.
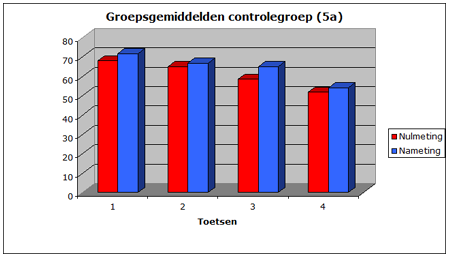
Figuur 1: de controlegroep
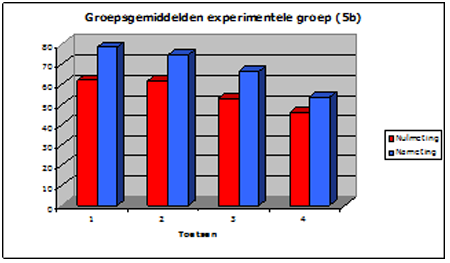
Figuur 2: de interventiegroep
In één oogopslag is te zien dat de experimentele groep een grotere vooruitgang op de tempotoetsen heeft geboekt. De achterstanden zijn ingehaald en bij drie van de vier toetsen zijn de achterstanden zelfs omgebogen in voorsprongen. In de controlegroep scoorden sommige kinderen tijdens de nameting lager dan tijdens de nulmeting. Zij waren dus in de maanden januari en februari zelfs achteruit gegaan, wat in de experimentele groep niet voorkwam.
Niet alleen nam de gemiddelde score van de experimentele groep toe, ook de SD (standaarddeviatie) nam af, wat betekent dat de spreiding van de scores minder groot was bij de nameting. Dit is vooral te zien bij toets 1 (optellen over het eerste tiental). Dit betekent dat met name de zwakke rekenaars profiteerden van de interventie. De goede rekenaars hielden hun hoge scores vast, maar gingen niet spectaculair vooruit, wat logisch is aangezien de toetsen een maximum score hebben en enkele leerlingen deze al bereikten bij de nulmeting. Tijdens de nameting is hun vooruitgang niet gemeten. Wel heeft de onderzoeker geobserveerd dat zij ruim binnen de minuut klaar waren met de opgaven en dus een hogere score hadden kunnen halen bij meer sommen.
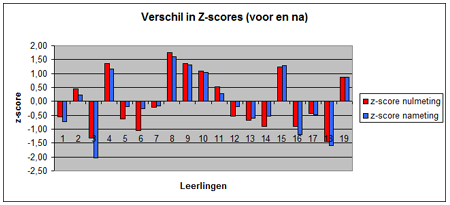
Daarnaast zijn ook de z-scores van de 19 leerlingen berekend die meededen met de voor- en nameting van de experimentele groep (zie onderstaand staafdiagram). Hieruit is af te leiden dat weliswaar alle leerlingen vooruit zijn gegaan in vaardigheid, maar dat de voorsprong die enkele leerlingen hadden ten opzichte van het gemiddelde wel kleiner werd (leerling 2, 4, 8, 9, 10, 11). Vijf leerlingen zagen hun achterstand ten opzichte van het gemiddelde van de groep toenemen (leerling 1, 3, 16, 17 en 18), terwijl vier leerlingen hun achterstand ten opzichte van het gemiddelde redelijk spectaculair zagen slinken (5, 6, 12 en 14).
Cito-toets in correlatie met tempotoetsen “automatiseren tot 100”
In januari werd bij deze leerlingen tevens de Citotoets rekenen M5 (LOVS, 2010) afgenomen en met behulp van de vaardigheidsscores op deze toets en de formule van de Pearson’s Productmomentcorrelatiecoëfficiënt (Van Peet en Everaert, 2009) heb ik de correlatie uitgerekend tussen de Cito-toets M5 (2010) en de tempotoetsen van Maatwerk Oranje (Erich, Galen en Huitema). De correlatie tussen deze twee toetsen is gelijk aan 0.64.
Omdat er geen eerdere gevonden waarde voor de correlatie tussen deze twee variabelen (Cito rekenen M5 (2010) en de tempotoetsen van Maatwerk Oranje (Erich, Galen en Huitema)) bekend is en het dus moeilijk is deze waarde te interpreteren, heb ik gebruik gemaakt van het percentage voorspelde variantie; dit is de gekwadrateerde correlatiecoëfficiënt vermenigvuldigd met 100. Deze bedraagt: 0.642x100=41%.
Dit betekent dat 41% van de verschillen in de Cito-toetsen voorspeld worden door de verschillen in de tempotoetsen van Maatwerk (Erich, Galen en Huitema). Men kan dus 59% van de verschillen niet voorspellen/verklaren (Van Peet en Everaert, 2009).
Dit lijkt een lage correlatie, gezien het feit dat het beide rekentoetsen zijn. Toch wil ik hier gelijk de beperking aangeven. De tempotoetsen van Maatwerk (Erich, Galen en Huitema) toetsen een zeer beperkt onderdeel van het rekenen en hebben dus een beperkte reikwijdte (restriction of range).
Tevens zijn het twee verschillende rekentoetsen; de één toetst zuivere sommen en bewerkingen binnen een bepaalde tijd, de ander (Cito) heeft een hoge verbale factor en toetst inzicht in het toepassen van de bewerkingen zonder tijdsbeperking.
De leerling-enquête
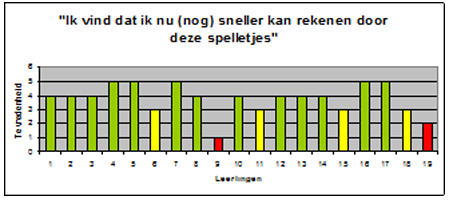
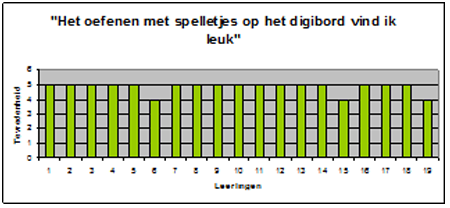
In deze enquête hebben de leerlingen hun mening gegeven over 9 stellingen die niet intern consistent zijn. Daarom heb ik de stellingen apart geïnterpreteerd en niet als geheel of als item. De belangrijkste stellingen zijn zo gesteld dat een hoge score samenhangt met een positieve attitude of competentiegevoel. Er hoefde dus niet omgescoord te worden (Van Peet en Everaert, 2009). In de grafieken zijn de positieve scores weergegeven met een groen, “er tussen in” met een geel staafje en een negatieve score met een rood staafje.
Alle kinderen (100%) vonden de oefeningen uitgevoerd met het digitale schoolbord erg leuk. Van de 19 kinderen vonden 13 kinderen dat ze na de interventie sneller zijn gaan rekenen (68%), 2 kinderen vinden dit niet en 4 kinderen (21%) vinden dat ze even snel rekenen.
(De coöperatieve en digitale werkvormen stonden bij de leerlingen bekend als “de rekenspelletjes”).
Conclusies en discussie
De tijdens het experiment gehanteerde oefenvormen lijken, in combinatie met de structureel coöperatieve werkvormen, tot een gunstig effect te hebben geleid van de beheersing van de basisvaardigheden van het rekenen tot honderd en vooral de zwakkere leerlingen hebben hier van geprofiteerd, gezien de afname van de standaarddeviatie. De keuze van een succesvolle oplossingsstrategie is een belangrijk onderdeel van de vaardigheid in automatiseren.
Onderzoek hiernaar werd gedaan door Milo in 2003 (Ruijssenaars et al., 2004). Milo maakt in dit onderzoek gebruik van twee strategieën bij het optellen en aftrekken tot honderd: de rijgstrategie en de splitsstrategie.
In dit onderzoek concludeert Milo dat zwakke rekenaars het minst profiteren van de splitsstrategie en het meest baat hebben bij de rijgstrategie. Een derde groep, waarin de leerlingen zelf inbreng hadden in hun strategiekeuze, scoorde ook lager.
In een onderzoek van Van Lieshout en Meijers (2002) genoemd door Ruijssenaars (2004) werden hoogbegaafde leerlingen vergeleken met drie jaar oudere leerlingen met rekenproblemen ten aanzien van de strategiekeuze bij sommen tot 100.
Ook zij vonden dat zwakke rekenaars vaker kozen voor de inefficiënte splitsstrategie. Ruijssenaars impliceert dat er niet alleen gekeken moet worden naar de prestatie in rekenniveau, maar ook naar het proces erachter: welke rekenstrategieën gaan er schuil achter een oplossing?
Verschillende onderzoeken tonen aan dat bij zwakke rekenaars een directe strategie-instructie te verkiezen is boven het bevorderen van eigen inbreng.
Vooral in de diagnostiek van rekenproblemen kunnen hierdoor handelingsgerichtere uitspraken worden gedaan die meer aansluiten bij de onderwijsbehoeften van een bepaalde leerling. Een juiste keuze kan alleen bereikt worden door een goede, excellente instructie (en bij zwakke rekenaars dus door een sturende didactiek) en door evaluatie van de oplossing.
De hogere scores van de leerlingen bij de optelsommen lijken voor een groot deel verklaard te kunnen worden door het frequentie-effect. Bij optelsommen (en ook bij keersommen) is sprake van het omkeerprincipe, waardoor de sommen vaker voorkomen dan aftreksommen.
Dit is een argument dat deze sommen eerder geautomatiseerd kunnen zijn dan minsommen. Des te opmerkelijker vind ik het dat de normen van de gebruikte tempotoetsen van Maatwerk (Erich, Galen en Huitema, n.d.) gelijk zijn voor zowel de optelsommen als voor de aftreksommen.
Veel scholen gebruiken geen landelijk genormeerde tempotoetsen. Ook de school waar dit onderzoek plaats vond niet. Hierdoor is het moeilijk om bij dit soort onderzoeken de leerresultaten te meten. In dit onderzoek is dit probleem omzeild door een voor- en een nameting te doen en de groepen met zichzelf en met elkaar te vergelijken.
Om grootschalige uitspraken te doen over het niveau van automatiseren en scholen met elkaar te vergelijken zou misschien een vakinhoudelijke discussie gevoerd moeten worden over de relevantie en eventuele noodzaak van het afnemen van een landelijk genormeerde tempotoets rekenen. Zeker gezien het feit dat het werkgeheugen wordt ontlast wanneer sprake is van vergaande automatisering van rekenfeiten en leerlingen dus toekomen aan complexere sommen, lijkt het geïndiceerd om deze vaardigheid op tijd in de kaart te brengen.
Literatuurlijst
Braams, T. en Denis, D. (2003). Getalbegrip: een noodzakelijke voorwaarde voor het leren rekenen. Tijdschrift voor Remedial Teaching, 2003.
Craats, Van de, J. (2007). Waarom Daan en Sanne niet kunnen rekenen. Nieuw Archief voor Wiskunde, 8, 132-136.
Erich, L., Galen, F. en Huitema, S. Maatwerk rekenen (Oranje).’s-Hertogenbosch: Malmberg.
Fuchs, L.S. (2006). Strategies to Enhance Young Children’s Mathematical Development. In Tremblay RE, Barr RG, Peters RDeV Eds. Encyclopedia on Early Childhood Development. Montreal, Quebec: Centre of Excellence for Early Childhood Development. 2006: 1-7.
Gelderblom, G. (2007). Effectief omgaan met verschillen in het rekenonderwijs. Amersfoort: CPS onderwijsontwikkeling en advies.
Gelderblom, G. (2008). Effectief omgaan met zwakke rekenaars. Amersfoort: CPS onderwijsontwikkeling en advies.
Kagan, S. (2004). Structureel Coöperatief Leren. Vlissingen: Bazalt.
Kerndoelenboekje. (2006). Publicatie van het Ministerie van Onderwijs, Cultuur en Wetenschappen.
Kole, L., Hoop, de V. en Riemens, C. (2009). Nog beter rekenen. Vlissingen: Bazalt.
Moerlands, F. & Straaten, Van der H. (2008). De ijsbergmetafoor.
Peet, Van A.A.J. & Everaert, H.A.M. (2009). Lessen in onderzoek. Amersfoort: Uitgeverij Agiel.
Roussel, J-L., Fayol, M., Barrouillet, P. (2002). Procedural vs. Direct retrieval strategies in arithmetic: A; comparison between additive and multiplicative problem solving. European Journal of Cognitive Psychology, 14, 61-104.
Ruijssenaars, A.J.J.M., Luit, van J.E.H. en Lieshout, van E.C.D.M. (2004). Rekenproblemen en dyscalculie. Rotterdam: Lemniscaat b.v.
Thevenot, C. en Barrouillet, P. (2006). Encoding numbers: Behavourial Evidence for processing-specific representations. Memory & Cognition 2006, 34 (4), 938-948.
Verschuren, P. en Doorewaard, H. (2004). Het ontwerpen van een onderzoek. Utrecht: Uitgeverij Lemma BV.