Wie kan delen, kan vermenigvuldigen
Martie de Pater
Rekenspecialist en onderwijsadviseur bij De Pater Onderwijsadvies
de Pater, M. (2014). Wie kan delen, kan vermenigvuldigen.
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/leerlijn-rekenen.php
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/leerlijn-rekenen.php
Geplaatst op 1 juni 2014

Kennis van leerlijnen is essentieel voor goed rekenonderwijs
Eerlijk delen is voor kinderen nooit een probleem. Al heel jong weten kinderen hoe ze een berg knikkers, pepernoten of blokjes eerlijk over diverse kinderen moeten verdelen. Toch blijkt de leerlijn delen voor veel kinderen grote problemen op te leveren.
Op basis van onderzoek onder leerkrachten worden in dit artikel belangrijke aspecten van de leerlijn delen besproken: de cruciale leermomenten, strategieën en modellen.
De rekenmethode is niet passend voor elke leerling. Leerkrachten zullen keuzes moeten maken in het aanbod van de methode. Om dit verantwoord te kunnen doen is inzicht in leerlijnen een voorwaarde. Het overzien van een complete leerlijn vraagt om een helikopterview waarbij men de leerlijn met haar modellen, strategieën en kernpunten (cruciale leermomenten) kan overzien. In een onderzoek onder leerkrachten kwam naar voren dat veel leerkrachten dit overzicht niet voor alle leerlijnen even goed kennen. In dit artikel zoomen we in op de leerlijn delen, een leerlijn die minder bekend is dan bijvoorbeeld de leerlijnen optellen en aftrekken. We beschrijven de leerlijn, cruciale leermomenten, de strategieën en modellen.
Leerlijn
Een leerlijn is een samenvoeging van enerzijds de leerstoflijn die aangeeft welke leerstof wordt behandeld en beheerst moet worden per jaargroep en anderzijds de onderwijslijn die aangeeft op welke manier de leerstof wordt geleerd (zie hiervoor ook de TAL- brochures). Hierin staan didactische aanwijzingen als materialen en modellen, als ook de verschillende hoofdlijnen binnen de leerstof centraal. Deze hoofdlijnen en hun relatie tot elkaar, wordt weergegeven in afbeelding 1.
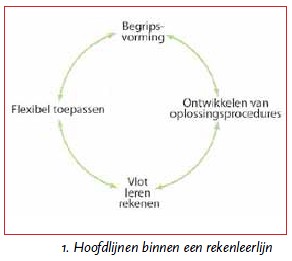
Elke leerlijn kent daarnaast ook cruciale leermomenten. Dit zijn als het ware eyeopeners voor kinderen om een niveauverhoging te kunnen doormaken binnen de leerlijn. De verschillende fasen van niveauverhoging zijn zichtbaar gemaakt in het zogenoemde handelingsmodel (afbeelding 2). In het geval van de leerlijn delen, verdelen leerlingen daadwerkelijk voorwerpen (fase ‘doen’).
In de volgende fase is deze werkelijkheid afgebeeld als foto of tekening (‘fase realistische denkmodellen’). De fase daarna wordt deze afbeelding geschematiseerd (fase ‘wiskundige denkmodellen’), waarna hij in de laatste fase plaatsmaakt voor de abstracte, formele notatie, bijvoorbeeld 24 : 6 (fase ‘symbolen’). Voor het begrip is het van belang bij elke fase te kunnen verwoorden wat er gebeurt. Dus zowel van concreet naar formeel als van formeel naar concreet.

Leerlijn delen
Welke achtergrondkennis is voor leerkrachten van belang bij het geven van een goede rekenles? In de kleutergroepen staat begripsvorming en het ontwikkelen van een bijpassende rekentaal als delen, verdelen en eerlijk delen centraal. Het verdelen van allerlei voorwerpen en daarbij verwoorden wat er gebeurt is daarom van groot belang. Deze begripsfase loopt door tot en met groep 3. Het is van belang dat leerlingen in de begripsfase in aanraking komen met zowel verdeelsituaties: ‘Er zijn 24 snoepjes die verdeeld moeten worden over 6 kinderen. Hoeveel snoepjes krijgt ieder?’ als opdeelsituaties: ‘Ik heb 24 snoepjes die ik in zakjes van 6 moet doen. Hoeveel zakjes kan ik vullen?’
Kinderen hoeven dit verschil niet te kunnen benoemen, maar er mee in aanraking komen is wel relevant om in een later stadium te begrijpen dat daardoor ook verschillende oplossingsstrategieën nodig zijn (zie afbeelding 3 en 4). Daarnaast is het van belang dat leerkrachten hun leerlingen helpen het besef te ontwikkelen dat delen in feite het herhaald aftrekken van eenzelfde hoeveelheid is. Dit is een cruciaal leermoment omdat dit de essentie van delen is. Bij het uitrekenen van deelsommen kunnen kinderen in deze fase de getallenlijn gebruiken.
In deze fase wordt het eerder genoemde verschil tussen verdelen en opdelen zichtbaar in de gehanteerde oplossingsstrategie. Bij een verdeelsituatie ga je uit van het geheel en verdeel je net zo lang tot het op is.

Verdeelsituatie
Bij een opdeelsituatie ga je uit van 0 en verdeel je net zo lang tot het op is. Je begint dus aan de andere kant. Leerkrachten die zich bewust zijn van welke deelsituaties er zijn, weten dat dit inzicht kan geven in mogelijke oplossingsstrategieën die een leerling kan hanteren om de deling uit te rekenen. Het is van belang om te weten dat in deze fase ook het formele deelteken wordt geïntroduceerd. Daarbij is het belangrijk om telkens de brug te blijven slaan tussen het abstracte en het concrete. Dus bij een verhaal of een plaatje de formele som kunnen noemen en bij een formele som een verhaal of plaatje kunnen bedenken. Deze overgang naar de formele notatie is een cruciaal leermoment. Naast het besef dat delen in feite herhaald aftrekken is, is het van belang dat leerlingen ook beseffen dat dit in verkorte vorm eigenlijk het tegenovergestelde is van vermenigvuldigen. Deze relatie wordt zichtbaar in opgaven als 24 : 4 hoe vaak past 4 in 24?
Sommige methoden bieden deze relatie al direct aan bij de introductie van het delen. In andere methoden komt dit na elkaar. Van Vught en Wösten (2004) beschrijven deze relatie heel treffend: ‘Je deelt uit (een geheel in delen) en je voegt ook weer samen (de delen naar een geheel).’ Als kinderen dit niet begrijpen, wordt ‘delen is het omgekeerde van vermenigvuldigen’ een trucje.

Cruciale leermomenten in de leerlijn delen
In de hierboven beschreven leerlijn delen komt een aantal cruciale momenten aan de orde, zoals:
• Het besef dat delen in feite herhaald aftrekken is.
• Begrip van het formele deelteken en dit kunnen gebruiken.
• Begrijpen dat delen hetzelfde is als omgekeerd vermenigvuldigen en dit toepassen.
• Kunnen delen met rest en het antwoord kunnen plaatsen in de context.
• Het begrip rest leren kennen.
• Begrip van het formele deelteken en dit kunnen gebruiken.
• Begrijpen dat delen hetzelfde is als omgekeerd vermenigvuldigen en dit toepassen.
• Kunnen delen met rest en het antwoord kunnen plaatsen in de context.
• Het begrip rest leren kennen.
Het kennen van het : symbool is ook een cruciaal leermoment. Het is een belangrijk schakelpunt tussen de concrete en de abstracte wereld. Leerkrachten stellen vaak vast dat de inverse relatie tussen vermenigvuldigen en delen (Bij elke keersom hoort een deelsom) door veel kinderen niet goed wordt toegepast. Het is dan ook van belang dat de leerlingen begrijpen waarom dit met elkaar in verband staat, anders verwordt het tot een trucje. En trucjes worden makkelijk door elkaar gehaald of vergeten. Het tegelmodel kan hier voor het nodige inzicht zorgen (zie hieronder: Modellen in de leerlijn).
Strategieën in de leerlijn delen
Elke leerlijn bevat mogelijke strategieën. Een strategie is een manier waarop je een som kunt uitrekenen. Binnen de leerlijn delen speelt een aantal strategieën een rol. In de middenbouw: het herhaald aftrekken bij verdeelsituaties en herhaald optellen bij opdeelsituaties. Bij de grotere delingen kan de splitsstrategie gebruikt worden en het rekenen naar analogie (210:7 via 21:7). In de bovenbouw kunnen delingen opgelost worden met behulp van de happenmethode (‘het nemen van de grootste hap’).
Voor leerlingen die dit goed beheersen is de traditionele staartdeling een mogelijke oplossingsstrategie. Bij het oplossen van een deling zie je tot slot dat kinderen ook het opvermenigvuldigen gebruiken als strategie.
Eenvoudige delingen kunnen opgelost worden met behulp van de getallenlijn (zie afbeelding 3 en 4). Wanneer het om grotere delingen gaat, is splitsen een efficiëntere strategie (364:7= 350:7 en 14:7). Ook het rekenen naar analogie kan in deze fase als strategie dienen: 21:7=3 dus 210:7=30. Bij beide strategieën is tafelkennis noodzakelijk. Naast verdeel- en opdeelsituaties komen er in de bovenbouw ook veel contexten bij waarin de deling niet helemaal opgaat. De zogenoemde ‘restsommen’. Bij restsommen is er verschil in het kale antwoord (bijvoorbeeld 7 rest 1) en het antwoord in de context (bijvoorbeeld 8 boten). Het kunnen delen met rest en daarbij het antwoord kunnen plaatsen in de context is een cruciaal leermoment. Het is van belang dat de leerkracht goed in de gaten heeft welke kinderen daar moeite mee hebben, omdat dit te maken heeft met het begrip.
Als het gaat om grotere delingen in groep 7 en 8 wordt ook gebruik gemaakt van analogie en daarnaast in eerste instantie van de happenmethode en daarna van de staartdeling.
Er kan bij van de happenmethode naar verkorting gewerkt worden door steeds grotere happen te nemen. Een andere, veelgebruikte oplossingsstrategie is het zogenoemde ‘opvermenigvuldigen’ of ‘schattend vermenigvuldigen’. Bij een opgave als 310:4, begint een leerling met 10x4 en gaan dan net zo lang door ‘iets’ keer 4 te doen tot ze bij 310 zijn. Dit gaat efficiënter naarmate ze de tafels beter kennen. Deze strategie wordt aangemerkt als een cruciaal leermoment omdat hierin de relatie tussen delen en vermenigvuldigen ook echt gebruikt wordt door de leerling.
Naast het delen zonder en met rest komen in de bovenbouw ook delingen met kommagetallen aan de orde. Dit gebeurt vaak in de context van geld. Om meer zicht te krijgen op de leerlijn is het is van belang te beseffen dat de opbouw over de gehele leerlijn verloopt via de fasen zoals weergegeven in het handelingsmodel: van concreet, via schematische weergave, naar formele sommen.
Modellen in de leerlijn delen Een model is een manier om de kloof tussen de concrete context en de formele som te overbruggen. Binnen de leerlijn delen zijn diverse modellen te onderscheiden. Allereerst de getallenlijn, ook wel een lijnmodel genoemd. Met behulp van de getallenlijn kunnen leerlingen herhaald aftrekken of optellen. Dit werd zichtbaar in het eerder genoemde voorbeeld van het verdelen van 24 snoepjes over 6 kinderen. De getallenlijn wordt voorafgegaan door de meer inzichtelijke kralenketting, waarbij de hoeveelheden ook echt nog zichtbaar zijn. Een tweede model is het tegelmodel. Het tegelmodel maakt de relatie tussen delen en vermenigvuldigen zichtbaar. Het tegelmodel laat een hoeveelheid zien die uit elkaar gehaald kan worden in gelijke delen, maar ook
weer samengevoegd kan worden tot een eenheid.
5. Rechthoek- of tegelmodel
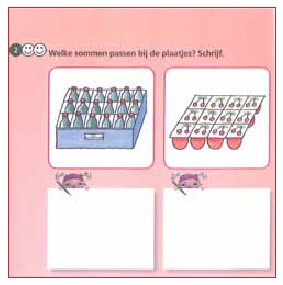
Een derde model dat gebruikt zou kunnen worden is het groepjesmodel. Ik heb bijvoorbeeld 18 eieren en ik heb eierdozen waarin in één doos 6 eieren kunnen. Hoeveel dozen heb ik nodig? Ook met dit model kun je de relatie tussen vermenigvuldigen en delen inzichtelijk maken.
Conclusie
Wanneer je een leerlijn kent, heb je met die kennis gereedschap in handen waarmee je op een goede manier je rekenlessen vorm kunt geven. Je weet dan welke momenten in een leerlijn belangrijk zijn en welke modellen en strategieën je kunt gebruiken tijdens je instructie. Daarnaast geeft deze kennis je sneller inzicht in het niveau waarop de leerling rekent en welke oplossingsstrategie een leerling hanteert. Passend onderwijs, preventie en snelle signalering van rekenproblemen kunnen op deze manier sneller gerealiseerd worden.
Het genoemde handelingsmodel en de hoofdlijnen kunnen als kapstok dienen om van daaruit een leerlijn met al zijn modellen, strategieën en cruciale leermomenten nader te verkennen. Dit vraagt om een bewuste keuze van scholen om alle leerkrachten schoolbreed zich te laten verdiepen in leerlijnen. Dat is niet alleen erg boeiend, maar op die manier werkt een school aan de kwaliteit van de rekenlessen waarin de leerkrachten kunnen inspelen op niveauverschillen tussen leerlingen. Dat je daarmee ook werkt aan preventie en snelle signalering van rekenproblemen, is mooi meegenomen!
Literatuur
- Tal team (1999). Jonge kinderen leren rekenen. Groningen: Wolters-Noordhoff.
- Heuvel-Panhuizen, M. van den, Buys, K., & Treffers, A. (2001). Kinderen leren rekenen. Tussendoelen annex leerlijnen. Hele getallen bovenbouw basisschool. Groningen: Wolters- Noordhoff.
- Vught, J.M.C.G. van, & Wösten, A. (2004). Rekenen: een hele opgave. Baarn: HB Uitgevers.
- Heuvel-Panhuizen, M. van den, Buys, K., & Treffers, A. (2001). Kinderen leren rekenen. Tussendoelen annex leerlijnen. Hele getallen bovenbouw basisschool. Groningen: Wolters- Noordhoff.
- Vught, J.M.C.G. van, & Wösten, A. (2004). Rekenen: een hele opgave. Baarn: HB Uitgevers.
Boek: Leren rekenen
Werken met de modellen uit het Protocol ERWD
Leren rekenen, ook als het moeilijk wordt
de modellen uit het protocol ERWD in de praktijk
Heb je vragen over dit thema? Stel ze in de onderwijs community binnen de Wij-leren.nl Academie!