Leren vermenigvuldigen: meer dan tafels leren!
Martie de Pater
Rekenspecialist en onderwijsadviseur bij De Pater Onderwijsadvies
Janson D. de Pater, M. (2014). Leren vermenigvuldigen: meer dan tafels leren!.
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/tafels-leren.php
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/tafels-leren.php
Geplaatst op 1 juni 2014

Dit artikel is mede geschreven door Dolf Janson, senior onderwijsadviseur en -ontwikkelaar bij APS.
Kennis van de tafels zakt weer weg
“Die tafels kennen ze nog steeds niet”, verzuchten veel leraren in de bovenbouw. Toch hebben hun collega’s in eerdere groepen veel aandacht aan de tafels besteed. Wat maakt dat (te) veel leerlingen die kennis ook weer snel kwijtraken?
In dit artikel zetten we dit verschijnsel in een breder kader en doen aanbevelingen. We gebruiken daarbij de drie modellen uit het protocol Ernstige RekenWiskundeproblemen en Dyscalculie (ERWD1): de vier Hoofdlijnen, het Handelingsmodel en het Drieslagmodel.
Het Hoofdlijnenmodel
Op de vraag waar het bij het leren van de tafels misgaat, noemen leraren meestal het paraat hebben van de tafelproducten. Dat valt op doordat leerlingen antwoorden op sommige tafelsommen niet paraat hebben en veel tijd nodig hebben om complexere vermenigvuldigen uit te rekenen. Wanneer we die klacht proberen te plaatsen binnen de vier hoofdlijnen voor leren rekenen, komen we terecht bij vlot leren rekenen. Daar doet zich blijkbaar het probleem voor en vervolgens gaat ook het flexibel toepassen minder goed.
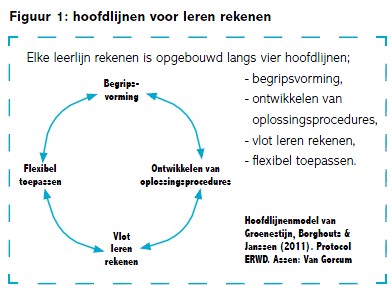
Vier fasen leerproces rekenen
Het Hoofdlijnenmodel is de weergave van vier fasen in het leerproces bij rekenen. Elke volgende fase veronderstelt de beheersing van de vorige. Dat maakt al direct duidelijk dat de oorzaak van de stagnatie bij de tafels niet pas begint in de fase van het vlot leren rekenen. Daarvoor waren ontwikkelde oplossingsprocedures nodig en daarvoor was weer begripsvorming noodzakelijk. Het signaleren van niet beheerste tafelsommen moet daarom niet leiden tot het dan maar instampen van die sommen. Dat zou symptoombestrijding zijn, die binnen de kortste keren weer herhaald moet worden. Laten we daarom gewoon bij het begin beginnen en bekijken wat er nodig is in de opeenvolgende stappen van de leerlijn vermenigvuldigen.
Fase 1: ontwikkelen van begrip
Vermenigvuldigen komt vaak voort uit herhaald optellen. De herhaalde toevoeging van steeds dezelfde hoeveelheid, daagt uit tot een snellere manier van rekenen. Het is wel noodzakelijk om juist bij de introductie niet te kleine aantallen te nemen. Die kunnen ze immers optellend ook snel uitrekenen. De noodzaak om op zoek te gaan naar een snellere manier is er dan niet. Je trakteert je groep op zakjes knikkers. In elk zakje zitten er vijf. Er zitten 25 kinderen in je groep. Hoeveel knikkers hebben jullie dan met elkaar?
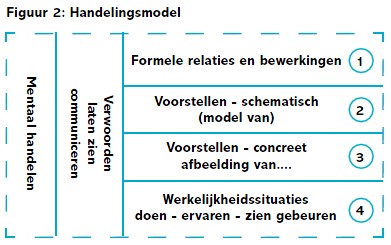
Deze situatie is volledig uit te spelen. Er zijn 25 zakjes met vijf knikkers. Je zou die knikkers steeds bij elkaar kunnen optellen, maar dat is veel werk. Kan het niet handiger? In het Handelingsmodel is dit niveau 4: handelen op concreet niveau, dus met echte bij de context passende voorwerpen (en niet met betekenisloze blokjes of iets dergelijks). Laat de leerlingen in tweetallen bedenken hoe dat handiger is uit te rekenen. De ideeën brengen ze onder woorden, kunnen worden uitgeprobeerd en met elkaar vergeleken. Iedereen kan meedoen.
Al die zakjes is een hoop gedoe. Daarom kun je kinderen digitale foto’s laten maken van de verschillende manieren waarop de kinderen de zakjes geordend hebben. Die kunnen zij later op het digibord of een tablet laten zien. Weet je nog wat we deden? Dit is handelingsniveau 3: een afbeelding die de werkelijkheid weergeeft. De leerlingen kunnen er niet meer mee manipuleren, maar er wel concreet aan terugdenken. Belangrijk daarbij is om de kinderen voor het bekijken uit te dagen er aan terug te denken, zodat ze een ‘mentaal beeld’ oproepen. Laat hen beschrijven wat ze ‘zien’! Wat was het probleem ook alweer?
Dit verhaal met de knikkers is een duidelijk voorbeeld van een groepjescontext. Daarom gebruik je bij dit soort verhalen het groepjesmodel om de werkelijkheid verder te abstraheren. Je tekent 25 rondjes met in elk een 5. Nu zien de leerlingen geen knikkers meer, maar de tekening herinnert daar nog wel aan. Dit is handelingsniveau 2, een model waarin de werkelijkheid schematisch is weergegeven. Alleen de essentiële kenmerken zijn over: 25 groepjes met in elk 5 ‘dingen’. Door erover te praten, door oplossingen uit te proberen kom je met de leerlingen ten slotte uit bij de formulering ‘25 groepjes van 5’ die je nog verder kunt verkorten tot ‘25 van 5’ en die je ten slotte als formule weergeeft met ‘25x5’. Nog steeds kunnen de leerlingen daar de groepjestekening bij denken, of de foto en zelfs de stapel zakjes met knikkers.
De formule, de ‘kale som’, is niveau 1 binnen het Handelingsmodel. Dat niveau ontleent zijn betekenis aan de niveaus daaronder. Daar horen dus beelden bij en woorden om die te beschrijven Ook dat hoort bij het gebruik van het Handelingsmodel.
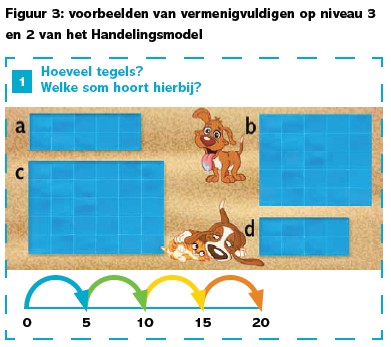
In de fase van de begripsvorming horen natuurlijk ook heel andere vermenigvuldigsituaties een plek te krijgen. Vaak gaat het niet om groepjes, maar om rechthoeken die steeds zijn verdeeld in gelijke rijen met dezelfde vlakken. Denk maar aan de kasten, de ramen en de postvakken op school. Daar past dan niet het groepjesmodel bij, maar het rechthoekmodel. Zo’n model in handelingsniveau 2 hoort te passen bij de beelden van de werkelijkheid die het model bij de leerlingen oproept.
Er is nog een derde soort situaties waarin vermenigvuldigen een rol speelt. Die zien we als de delen als het ware (of zelfs heel concreet) in elkaars verlengde liggen. Dan kun je denken aan de Avondvierdaagse, waar je elke avond 5 of 10 km loopt. Na vier avonden heb je dan een afstand van 20 of 40 km afgelegd. Zo’n afstand past niet bij het groepjesmodel en evenmin bij het rechthoekmodel. Hiervoor gebruiken we het lijnmodel: de afstanden liggen achter elkaar op een (getallen- of meet)lijn.
Begrip van vermenigvuldigen
Begrip van vermenigvuldigen ontwikkelen lukt het best als de leerlingen:
- de fasen van het Handelingsmodel systematisch doorlopen;
- met het vermenigvuldigen kennis maken vanuit heel verschillende contexten en daardoor ook verschillende modellen;
- steeds weer oefenen in het verwoorden van wat ze doen en zien, zodat de verbanden steeds duidelijker worden en verbonden zijn met het denken en onthouden;
- leren de samenhang tussen een context en het bijbehorende model te herkennen en benoemen.
- de fasen van het Handelingsmodel systematisch doorlopen;
- met het vermenigvuldigen kennis maken vanuit heel verschillende contexten en daardoor ook verschillende modellen;
- steeds weer oefenen in het verwoorden van wat ze doen en zien, zodat de verbanden steeds duidelijker worden en verbonden zijn met het denken en onthouden;
- leren de samenhang tussen een context en het bijbehorende model te herkennen en benoemen.
Door vanuit niveau 4 de concrete handelingen van leerlingen stap voor stap te laten uitgroeien tot de kale som, ontwikkelen de leerlingen begrip. Ze begrijpen waar die som naar verwijst en herkennen daarin een beeld van de werkelijkheid. Deze basis is essentieel en daarom moeten de leerlingen daarin zelf actief kunnen zijn. Dat betekent dat het niet genoeg is om het als leraar voor te doen en zelf maar snel de conclusie te noemen. Dat lijkt tijdwinst, maar het gevolg is dat juist de leerlingen die het van de rekenlessen moeten hebben, direct al verdwalen. Om het dan weer te repareren, kost heel veel meer tijd, vraag maar aan de collega’s van de bovenbouw...
We benadrukken het belang van een actieve rol voor de leerlingen tijdens het leerproces. Laat leerlingen zelf op zoek laten gaan naar vermenigvuldig- en/of deelsituaties in en om de school en die fotograferen. Dat blijkt een prima manier om leerlingen concepten, zoals vermenigvuldigen, te laten ontwikkelen en aan te scherpen.
In de begripsfase is het ook van belang aandacht te besteden aan de samenhang tussen vermenigvuldigen en delen. Dat kan meestal heel goed met dezelfde contexten. Die directe koppeling is niet alleen efficiënt, maar vooral van belang voor een goede begripsvorming van beide processen. Daarbij is het gegeven dat zowel de deling als de vermenigvuldiging weergegeven wordt met precies dezelfde getallen, een verrassende ontdekking voor veel leerlingen. Dat maakt later het onthouden een stuk eenvoudiger.
Fase 2: ontwikkelen van procedures
Van de introductie van het begrip ‘vermenigvuldigen’ overstappen naar het aanleren van tafels, lijkt een logisch vervolg. Toch ervaren leerlingen dat regelmatig als iets geheel nieuws. Als leraar moet je je realiseren dat een tafel een oplossing is. Maar als de leerlingen niet eerst ontdekt hebben welk probleem daardoor wordt opgelost, wordt de oplossing voor hen het probleem. Dat is een valkuil waar ook rekenmethodes regelmatig intuimelen. Vanuit de contexten uit de fase van begripsvorming kun je het zoeken naar antwoorden problematiseren. ‘Als je weet hoeveel knikkers er in 5 zakjes zitten, zouden we dan snel erachter kunnen komen hoeveel het er in 10 zakjes zijn?’ Van daaruit kunnen dan steeds meer vermenigvuldigingen ‘gevonden’ worden. Zo ontstaat al handelend een rij van sommen, direct gelinkt aan de voorwerpen uit de context. In het knikkerprobleem is het vanzelfsprekend om ook 20x5 en 25x5 te benoemen. Dat is helemaal niet erg, integendeel. Het is maar een traditie om een tafel te laten stoppen bij 10x.... Maar tafel betekent niets anders dan tabel en die mag je eindeloos verlengen, als dat nuttig is....
Van hieruit is de overstap te maken naar het construeren van tafels van vermenigvuldiging. Leerlingen die dat snel door hebben, maken parallel daaraan de tafels van deling! In deze fase gaat het nog niet om het kennen van de antwoorden, maar om het herkennen en snappen van het verband tussen de sommen, maar ook tussen verschillende tafels.
Vanuit het leerproces bezien, moeten leerlingen in deze fase nog veel uitproberen en onder woorden brengen. Te snel overstappen naar ‘antwoorden invullen’, leidt dan tot optellen in plaats van vermenigvuldigen. De opbrengst in deze fase is niet dat leerlingen tafelproducten kennen, maar dat ze de route kunnen aangegeven van een bekende tafelsom naar een nog niet bekende som. ‘Om 7x5 te vinden gebruik ik 5x5 (want die weet ik al) en 2x5 (want die is ook makkelijk). Dat is samen 7 groepjes van 5.’
Zo ontstaat al werkend en overleggend een patroon van handige manieren om bekende sommen te gebruiken om andere te vinden.

Steeds horen daar ‘plaatjes’ bij, mentale voorstellingen die de leerlingen kunnen oproepen doordat ze daar in de voorgaande fase uitgebreid zelf mee aan het werk zijn geweest. De idee dat het genoeg is om de tafel compleet op het bord te zetten en vaak te herhalen, gaat voorbij aan hoe leren plaatsvindt. Het is zoiets als iemand die zonder kaartbeeld een rijtje plaatsen uit zijn hoofd leert en hoopt zo de weg te kunnen vinden. Dat gaat meestal mis.... Het is niet genoeg om tafelsommen van buiten te leren. Daarvoor is het geheugen te kwetsbaar. Eerst moet er een degelijke basis zijn van begrijpen en mentale voorstellingen. Daarmee kunnen leerlingen altijd weer terugvallen op de betekenis. Daarom noemen we deze manier van aanleren ‘reconstructiedidactiek’.
De leerlingen vinden de tafels als het ware zelf opnieuw uit. Dat lijkt misschien omslachtig, maar is op de wat langere termijn een waardevolle investering: het resultaat is veel duurzamer en flexibeler. Wie vindt, of zelfs in het team heeft afgesproken dat alle tafels in groep vier gekend moeten zijn, zou ook eens moeten nagaan hoe de basis voor die tafels is gelegd. Hoeveel tijd en aandacht is besteed aan de eerste twee hoofdlijnen, begripsvorming en ontwikkelen van oplossingsprocedures?
Een leerling die geen beeld heeft bij 10x9, zal ook niet begrijpen dat je daarmee 9x9 kunt vinden. Het ontwikkelen van vaste procedures om tafelsommen uit te rekenen staat of valt met dit soort voorkennis. Daarnaast moeten leerlingen wel in staat zijn de optel- en aftreksommen die hiermee samenhangen uit te rekenen. Om 9x7 te vinden via 10x7, moet je wel 70-7 kunnen uitrekenen.

Leren direct te herkennen via welke hulpsom je een gevraagde tafelsom kunt vinden, noemen we automatiseren. Wie de tafels geautomatiseerd heeft, speelt met de strategieën uit figuur 4. Door het gebruik slijpen ook van steeds meer sommen de antwoorden al in. Een oefening in deze fase is bijvoorbeeld: twee leerlingen hebben losse kaartjes met keersommen. Om beurten pakken ze een kaartje en noemen zo snel mogelijk de hulpsom die ze hier kunnen gebruiken.
Dan zijn er drie mogelijkheden:
- Ik heb hier geen hulpsom nodig want ik weet het antwoord direct.
- Ik herken direct welke hulpsom hier handig is.
- Ik herken niet direct welke hulpsom ik hier kan gebruiken.
- Ik heb hier geen hulpsom nodig want ik weet het antwoord direct.
- Ik herken direct welke hulpsom hier handig is.
- Ik herken niet direct welke hulpsom ik hier kan gebruiken.
Zo ontstaan drie stapeltjes. Het laatste stapeltje vraagt het eerst om oefening. Met behulp van een overzicht als in figuur 4 kunnen twee leerlingen samen bespreken wat handig zou zijn.
Het tweede stapeltje is daarna aan de beurt. Welke van die sommen zou ik al snel zonder hulpsom kunnen weten? Dat is de stap op weg naar memoriseren. Dat is de fase waarin tafelsommen feitenkennis zijn geworden.
Fase 3: vlot leren rekenen
De derde hoofdlijn krijgt op school meestal de meeste aandacht en tijd. Vlot leren vermenigvuldigen is een fase in een leerproces en is eigenlijk niet ‘los verkrijgbaar’. Juist leerlingen die zich flink moeten inspannen om te leren rekenen, zijn heel kwetsbaar en gevoelig voor slordig toegepaste didactiek. Als in de beleving van zo’n leerling veel tafelproducten op zichzelf staan, blijft alleen uit het hoofd leren over. Dan is het ‘slechts’ een kwestie van inslijpen en onthouden, lijkt het. Veel losse feitjes zonder verband doen echter een extra beroep op het werkgeheugen. Geen wonder dat zwakke rekenaars vaak kampen met een overbelast werkgeheugen en dan verdwalen in losse, onbegrepen deelstappen. Het loont daarom de moeite vanaf het begin de zaak goed aan te pakken.
Wanneer leerlingen eerst het begrip vermenigvuldigen inhoud hebben gegeven en daardoor de oplossingprocedures met begrip kunnen toepassen, zijn zij minder kwetsbaar. Dat geeft hen zelfvertrouwen en daardoor kan het automatiseren van de procedures steeds vlotter gaan. De stap naar vlot rekenen is dan niet meer zo groot. Snelheid in uitrekenen vraagt daarna wel om onderhoud.
Fase 4: flexibel toepassen
De vierde hoofdlijn maakt de cirkel rond. Vlot en met begrip leren rekenen gebeurt immers om dat te kunnen toepassen. In de Referentieniveaus is sprake van ‘functioneel gebruik’ als doel van leren rekenen. Het venijn schuilt in die woordjes ‘flexibel’ en ‘functioneel’. Wie dat wil kunnen, moet tot meer in staat zijn dan rijtjes kale sommen uitrekenen. Er blijkt in de praktijk een groot verschil tussen leerlingen die kunnen rekenen en leerlingen die alleen hebben geleerd om sommen te maken.
Stel dat je aan het eind van groep 4 vraagt hoeveel 14x9 is. Zouden ze daarvan opkijken? Je mag het ook omkeren: hoeveel is 9x14? Zouden er leerlingen zijn die denken of zeggen ‘Die tafel hebben we toch nog niet gehad?’. Natuurlijk gaan leerlingen rekenen en komen er ook wel uit. Misschien hebben ze al wel geleerd hoe dat moet: eerst 10x of x10 en dan de rest (9x4 of 4x9). Interessant is dan of ze dat ook voor zich zien.

Het toepassen van de tafelkennis komt ook aan de orde in bijvoorbeeld (kale) opgaven als 2130:70. Herkennen de leerlingen hoe ze daarin tafelkennis kunnen gebruiken? Of liever nog: herkennen ze in deze deling de bijbehorende vermenigvuldiging? Zien ze snel of er een rest overblijft of niet? Flexibel toepassen is ook: vermenigvuldigsituaties en deelsituaties herkennen in een context.
De ramen van de school worden in de vakantie gewassen, van binnen en van buiten. Alle 8 lokalen zijn gelijk en hebben elk drie grote ramen. Elk raam ziet er zo uit. Om een ruitje uit zo’n raam aan een kant te wassen rekent het schoonmaakbedrijf € 0,50. Hoeveel moet de school betalen?
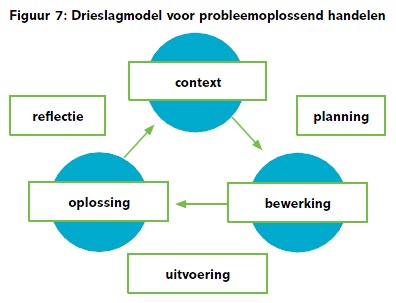
Bij dit type opdrachten is het Drieslagmodel voor probleemoplossend handelen (zoals het voluit heet), handig. De valkuil voor veel leerlingen is dat ze direct gaan rekenen. De valkuil van sommige leraren is trouwens ook dat ze hun leerlingen helpen door ze direct te laten rekenen (‘Wat moet je uitrekenen? Wat doe je eerst?’). Om een probleem goed te kunnen oplossen, is het verstandiger om eerst eens te kijken wat het probleem eigenlijk is. Waar gaat het over? Wat gebeurt er? Wat vragen ze eigenlijk? Welke getallen spelen een rol en welke rol dan?
Door systematisch de stappen van het Drieslagmodel te volgen, leer je de leerlingen altijd te beginnen met dit soort vragen. Dat is niet alleen handig bij een Cito-toets... in het voorbeeld kunnen de leerlingen als ze de genoemde vragen hebben beantwoord, bedenken hoe ze het (handig) kunnen aanpakken. Pas daarna komt het rekenwerk. Ten slotte is er de check: heb ik dat goed gelezen? Heb ik het handig aangepakt? Heb ik alle getallen goed gebruikt? Is het antwoord dat ik heb ook het antwoord dat werd gevraagd?
Ten slotte
De simpele verzuchting over tafelkennis vanuit de bovenbouw, leidde tot een uitgebreide uitleg over hoe leren vermenigvuldigen eigenlijk in zijn werk gaat. Het is daardoor iets ingewikkelder om op te lossen dan het geven van de aansporing ‘Je moet nog maar eens flink oefenen!’. Het vraagt om weldoordacht handelen in de groepen 4 en 5. Het vraagt ook om te doorzien hoe de rekenmethode hiermee omgaat. De roep om snelle tafelkennis heeft uitgevers ertoe verleid wat snel door die eerste twee hoofdlijnen heen te gaan. Dat is niet erg als je dat als leraar in die groepen maar herkent en je eigen plan trekt. Misschien is dat een mooi onderwerp om eens in een praktische bouwvergadering aan de orde te stellen.
Bronnen
- Inmiddels (najaar 2012) zijn er ook een ERWD2 (voor vo en vso) en een ERWD3 (voor mbo) ontwikkeld (M. van Groenestijn, G.J. van Dijken & D.J. Janson 2012). Uitgever: Van Gorcum (Assen)
- Janson, Dolf (2011). En de opbrengst is... In: Volgens Bartjens 31 nr 2 (2011-2012). Assen: Van Gorcum
- Janson, Dolf (2011). En de opbrengst is... In: Volgens Bartjens 31 nr 2 (2011-2012). Assen: Van Gorcum
Boek: Leren rekenen
Werken met de modellen uit het Protocol ERWD
Leren rekenen, ook als het moeilijk wordt
de modellen uit het protocol ERWD in de praktijk
Heb je vragen over dit thema? Stel ze in de onderwijs community binnen de Wij-leren.nl Academie!