Spelen of Toetsen
Kansen voor wiskundige ontwikkeling
Kleuters die problemen handelend weten op te lossen, blijken ook beter te scoren op de Citotoets ‘Rekenen voor kleuters’. Dit artikel laat zien hoe leerkrachten de kleuterwiskunde van het niveau van informeel handelen naar het niveau van concreet voorstellen kunnen begeleiden. Er wordt gewerkt met een praktijkvoorbeeld aan de hand van het Handelingsmodel uit het protocol ERWD.
Eén van de meest gehoorde bezwaren die kleuterleerkrachten hebben tegen de Citotoets ‘Rekenen voor kleuters’, is dat deze toets niet aansluit op de manier waarop er in de kleutergroepen wordt gewerkt. Kinderen van deze leeftijd leren immers vooral door middel van spel en manipuleren met materiaal.
De toets is echter op het platte vlak en sluit daarom in de beleving van leerkrachten niet aan bij de manier van werken in groep 1 en 2.
De kloof tussen handelen en voorstellen.
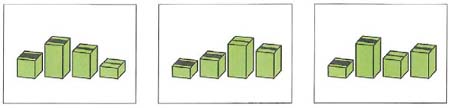
Onderstaande opgave komt uit het opgavenboekje van groep 2. Bij de opgave hoort de volgende tekst: Hier zie je blokken met strepen erop. Op welk plaatje staan de strepen van breed naar smal? Zet een streep onder dat plaatje.
Opgave uit de toets 'Rekenen voor kleuters' groep 2
Alle opgaven uit de toets ‘Rekenen voor kleuters’ bestaan uit een vraag met drie of vier getekende antwoordalternatieven. De leerkracht biedt de opgaven mondeling aan. De leerlingen antwoorden door een streep onder één van de afbeeldingen in hun opgavenboekje te zetten (Koerhuis, 2010, p. 5)
Het handelingsmodel
Handelingsmodel
Het handelingsmodel laat goed zien waarom leerkrachten een kloof ervaren tussen de toets en hun dagelijkse onderwijspraktijk. De opgaven van de toets bevinden zich op het niveau van voorstellen concreet, maar in kleutergroepen wordt veel gewerkt op het onderste niveau: het zogenoemde informeel handelen. De meeste kleuters kunnen de overstap van het ene niveau naar het andere niet zelf maken.
Zoeken naar verbinding
Een veelgehoorde oplossing is dat leraren besluiten tijdens de speelwerktijd leerlingen werkbladen laten maken zodat ze vast kunnen wennen aan het werken op het platte vlak. Veel leerkrachten ervaren dit als een noodgreep is die geen recht doet aan de manier van leren van jonge kinderen en is in veel gevallen niet bevorderlijk voor het werkplezier van zowel leerkracht als leerling.
Maar hoe overbrug je deze kloof? Het antwoord op deze vraag is ook te vinden in het handelingsmodel. Langs de vier handelingsniveaus staat het verwoorden als cruciale activiteit. Het verwoorden verbindt het ene handelingsniveau met het andere (de Pater – Sneep & Janson, 2012). Het volgende praktijkvoorbeeld laat zien hoe het informeel handelen en het concreet voorstellen met elkaar verbonden kunnen worden. De activiteit was inspirerend door de sterke betrokkenheid van de leerlingen, de differentiatiemogelijkheden, de ruimte voor vervolgactiviteiten en de diverse rekendoelen die in de activiteit aan bod kwamen.
De plattegrond
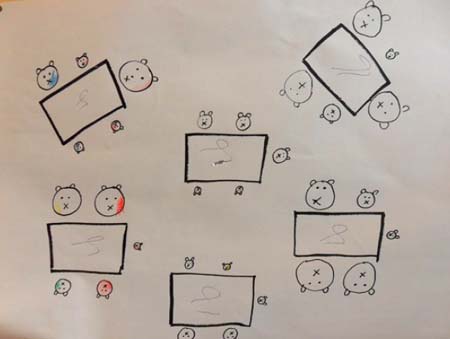
De plattegrond voor de k(r)oning
De activiteit in groep 1/ 2 vond plaats in de week waarin de troonswisseling plaatsvond. In de klas werd al langere tijd gewerkt rondom een troonswissel in een berenkoninkrijk. De leerkracht introduceerde de activiteit door te vertellen dat er na de inhuldiging een diner voor de belangrijkste gasten is in het paleis. ‘Er is een plattegrond gemaakt waarop staat waar alle beren moet gaan zitten en nu hebben ze ons gevraagd om te helpen alles zo neer te zetten volgens de plattegrond om te kijken of het allemaal goed staat.’
Allereerst wordt met elkaar de plattegrond verkend. De leerkracht stelt vragen als: Wat zijn die rechthoeken? Waarom zijn niet alle beren even groot? Waarom zijn er beren ondersteboven getekend? Hoeveel beren zitten er aan de middelste tafel? Daarna mogen om de beurt een aantal kinderen een tafel en de bijbehorende beren neerzetten. De plattegrond hangt op het bord en de beren komen op de tafel.
Het pakken van de goede maat beer gaat de meeste kinderen goed af. Moeilijker is het om de tafel en de beren volgens de plattegrond neer te zetten. Loïs bijvoorbeeld, mag de tafel die linksboven op de plattegrond staat getekend neerleggen. Ze staat tussen de tafel en de plattegrond en kijkt eerst goed op de plattegrond waar de tafel moet komen. Enthousiast draait ze zich vervolgens om en legt het rechthoekige blokje linksboven op de tafel. Een aantal leerlingen ziet dit en roept: Hé hij moet niet daar, hij moet daar! De kinderen wijzen vervolgens naar wat zij zien als de linkerbovenhoek. Dit gebeurt vervolgens ook een paar keer bij het neerzetten van de beren door andere leerlingen.
De tafelschikking van de berentafels
Ontdekkingen doen
Op de plattegrond zit links een grote beer en rechts een kleine beer. De leerlingen draaien zich om naar de tafel en leggen dit zo neer. Maar de kinderen die de tafel en de plattegrond voor zich hebben zien dat de grote beer rechts komt te zitten en de kleine beer links. Hoe komt dat? De leerlingen zitten in een rekenconflict. Al pratende komen de leerlingen erachter dat het uitmaakt waar je staat. Als je tussen de tafel en de plattegrond in staat, leg je het goed neer, maar iemand die aan de andere kant van de tafel zit ziet het dan omgekeerd. Het is dus belangrijk om af te spreken vanuit welke kant je kijkt.
Het beste is om de tafel naar de muur toe te schuiven, onder de plattegrond en dat je dan voor de tafel en de plattegrond komt te staan. Al puzzelend zijn de leerlingen bezig te schakelen tussen het platte vlak (voorstellen concreet) en het plaatsen van de tafels en beren (informeel handelen). De leerkracht stelt vragen om deze verbinding nog sterker te maken:
• Waar zie je de tafel die hier op de plattegrond staat op de berentafel?
• Wijs op de plattegrond eens deze berentafel aan?
• Wijs op de berentafel eens de tafel aan met de meeste kleine beren.
• Waar zie je deze tafel op de plattegrond?
• ……
Tot slot geeft de leerkracht de opdracht te tellen hoeveel gasten de koning eigenlijk heeft uitgenodigd. De betere rekenaars geeft ze op dit moment de opdracht uit te zoeken van welk soort gast (grootte en kleur) er het meest zijn en ze moeten daarbij ook laten zien hoe ze dit hebben uitgezocht.
Resultaat van de activiteit
Betrokkenheid
De betrokkenheid tijdens de activiteit was bij alle leerlingen erg hoog. Ze keken goed met elkaar mee als er wat werd neergezet en reageerden als er zaken niet klopten naar hun idee. Maar ook na de activiteit bleek hun betrokkenheid. De volgende dag kreeg de leerkracht nog suggesties en vragen als: ‘We kunnen de plattegrond misschien wel opsturen naar de echte koning’. ‘We moeten nog een stoel voor de koning op de plattegrond maken want die is er nog niet’.
De leerkracht besloot om nog een vervolgactiviteit uit te voeren rond de plattegrond. De tafel met beren werd in de kring gezet. De leerlingen moesten hun ogen dicht doen. De leerkracht verwisselde een aantal beren of liet er een paar helemaal weg en de leerlingen moesten met behulp van de plattegrond achterhalen wat er veranderd was.
Rekendoelen
Tijdens deze activiteit kwamen diverse rekendoelen aan bod:
• Begrippen met betrekking tot lengte en oppervlakte herkennen in betekenisvolle situaties (groot – groter – klein(ste) – kleine – enzovoort
• Tegenstellingen herkennen en gebruiken (grootste – kleinste) herkennen en gebruiken van meetkundige begrippen (voor – achter – naast – links – rechts – tussen - etc.)
• Kunnen redeneren over eenvoudige meetkundige problemen/conflictsituaties rond oriënteren en lokaliseren
• Eenvoudige plattegronden kunnen lezen, kunnen tekenen en kunnen toelichten
|
Hoe nu verder?
Het beschreven praktijkvoorbeeld laat zien dat er in de kleutergroep op een goede manier verbinding gelegd kan worden tussen het concreet voorstellen en informeel handelen. De kern hierbij is, is dat er geen keuze gemaakt hoeft te worden tussen handelend bezig zijn of werken op het platte vlak, maar dat beide lagen tegelijkertijd aan bod komen en deze met elkaar verbinden. Het vraagt om een verdiepte manier van kijken naar je rekenactiviteiten. Aan het werk rond het thema schoenenwinkel? Niet alleen laten uitzoeken van welke maat er de meeste schoenen zijn (informeel handelen) maar dit ook laten weergeven in de vorm van bijvoorbeeld een staafdiagram (voorstellen).
Maar dan ook weer vanuit een staafdiagram (voorstellen) terugredeneren naar de schoenen (informeel handelen). Het is de moeite waard om binnen een thema eens na te gaan bij welke activiteit(en) je de verbinding kunt leggen met een hoger of lager handelingsniveau en welke vragen je kunt stellen om deze verbinding te laten plaatsvinden.
Deze manier van werken doet recht aan het informeel leren dat zo past bij jonge kinderen, maar maakt ook dat ze steeds beter in staat zijn concrete situaties te vertalen naar het platte vlak en situaties op het platte vlak kunnen vertalen naar het concrete handelen. Op deze manier groeien ze toe naar een steeds verdere mate van het kunnen abstraheren van de werkelijkheid. Niet oefenen voor een toets dus, maar werken aan wiskundige ontwikkeling, want ook kleuters kunnen probleemoplossend aan het werk. En het is dan mooi meegenomen dat ze hier profijt van hebben bij een toets als Rekenen voor kleuters.
Met dank aan Lydia Schuurman, werkzaam in groep 1 – 3 op basisschool Steenenkamer in Putten
Literatuur
- Koerhuis, I. (2010). Van welk kind is deze schaduw? Nieuwe toets rekenen voor kleuters van Cito. Volgens Bartjens, 30 (2), 4 – 7.
- Pater- Sneep, M. de & Janson, D. (2012).
Vermenigvuldigen meer dan tafels leren. Pulse primair onderwijs, 4 (4), 12-16.