Leren denken als een programmeur (2)
Marléone Goudswaard
Ontwikkelaar en adviseur bij CED-groep
Geraadpleegd op 19-09-2024,
van https://wij-leren.nl/leerlijn-denken-als-een-programmeur.php

Deel 2: De vijf denkprocessen in één leerlijn
Het eerste artikel leest u hier.
Leerlijnen vormen de ruggengraat van het onderwijs. Ze zijn onmisbaar bij het realiseren van hoge en doelgerichte onderwijsopbrengsten.
Met behulp van een leerlijn kan je het denken als een programmeur inbedden in de dagelijkse lespraktijk, en er gericht ‘tools’ bij kiezen.

Afbeelding 1: Er zijn veel leuke programmeertools voor het onderwijs gemaakt. Kinderen ervaren de lol van het ontwikkelen. Een leerlijn geeft richtlijnen voor het aanbod.
Voor denken als een programmeur heeft de CED-Groep een doorgaande lijn ontwikkeld. De nadruk ligt in de lijn op de denkprocessen. Programmeren is daarom niet als een apart onderdeel, maar voorbeeldmatig opgenomen.
De leerlijn bevat doelstellingen voor de onder-, midden en bovenbouw van het primair onderwijs, op de volgende vijf onderdelen:
- Patroonherkenning
- Algoritme
- Abstractie
- Decompositie
- Data en classificatie
Wil je echt goed met de leerlijn kunnen werken in de klas, dan is het belangrijk om de essentie van de vijf onderdelen in de leerlijn goed te begrijpen: om welk denkproces gaat het precies en wat is de functie ervan? We beginnen onze verkenning bij patroonherkenning.
Patroonherkenning
.jpg)
Afbeelding 2: Patronen zijn overal om ons heen: letters en cijfers bestaan uit een aantal vormen zoals de lange stok en het rondje, muziek heeft een ritme, een dag heeft een vaste indeling in ochtend, middag, avond en nacht en we kennen vier seizoenen. Jonge kinderen maken al vroeg kennis met deze patronen.
Naarmate kinderen zich ontwikkelen, zijn zij in staat om steeds ingewikkeldere patronen te herkennen. Zoals spellingregels of rekenkundige oplossingen die volgens een vast patroon doorlopen. Dat is heel handig, want als je dit soort patronen herkent, kun je ook gebruik maken van oplossingen die al eerder zijn bedacht.
Barcode en QR code

Afbeelding 3
Bij patroonherkenning gaat het om het herkennen van gemeenschappelijke patronen in problemen, processen, oplossingen of data. Twee concrete voorbeelden van patroonherkenning in technologische oplossingen die de meeste kinderen wel zullen herkennen, zijn:
- de barcode;
- de QR code.
Met kinderen kun je onderzoeken doen naar de patronen. Waaruit bestaan ze, waaraan kun je ze herkennen?
.jpg)
Afbeelding 4
Lesidee patronen
Lesidee in kleurraster
Onderzoek als een rechercheur de vingerafdrukken van alle kinderen in de klas.
De afdrukken zijn uniek, geen afdruk is hetzelfde. En toch zien we allemaal dat het een vingerafdruk is.
- Waar herken je een vingerafdruk aan?
- Wat is het patroon?
- Hoe zou de rechercheur een scanner kunnen ontwerpen die de vingerafdrukken herkent?
Patronen bestaan niet alleen in concrete dingen zoals een barcode, QR code of vingerafdruk, maar ook in gebeurtenissen of acties die elkaar opvolgen. Zoals periodes en gebeurtenissen in de geschiedenis, stromingen in de kunst, een schaakspel, of zelfs bij een ruzie op het schoolplein.
Patronen zijn ook te vinden in informatie zelf, zoals de netnummers in een telefoonnummer, postcodes of de opbouw van het kenteken op de auto. Er zijn dus genoeg aanknopingspunten om de aandacht van kinderen te richten op patronen in hun dagelijkse omgeving.
Algoritme
.jpg)
Afbeelding 5: Bij een algoritme leren kinderen om heel precies te zijn in hun instructies. Want dan alleen kan een computer de opdrachten uitvoeren.
Een algoritme is een ondubbelzinnige instructie, of een precies stappenplan om een probleem op te lossen of een doel te bereiken.
Een algoritme wordt wel eens vergeleken met een recept: als je een recept voor chocoladecake opvolgt, levert je dat een chocoladecake op.
In theorie lijkt dat aardig.
- Maar waarom mislukt mijn cake dan toch?
- En is die van jou goed gelukt?
- Er staat ‘op smaak brengen…’
- ‘voeg een eetlepel suiker toe…’
- en wat dacht u van ‘een snufje zout’?
Deze instructies zijn niet heel precies. Bovendien worden er stappen overgeslagen, zoals een instructie voor hoe je een oven voorverwarmt.
Lesidee algoritme
Dit lesidee hoort bij het stukje over cake en de foto van eitje breken.
Lesidee in kleurraster
Laat kinderen in groepjes met hetzelfde recept aan de slag gaan. Bespreek met de kinderen hoe ze het hebben aangepakt en wat de resultaten zijn.
Welke overeenkomsten en verschillen zien de kinderen?
Op welke manier kan het recept aangepast worden zodat de resultaten meer op elkaar lijken?
Snelle oplossing
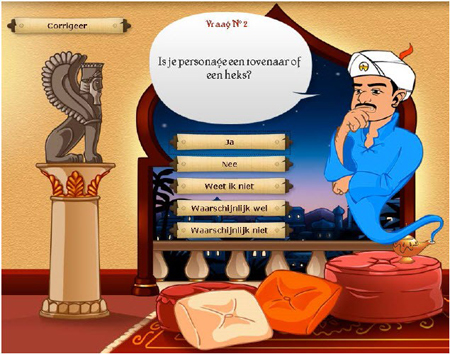
Afbeelding 6: Akinator is de digitale genie uit de fles. Hij raadt het personage dat kinderen in hun hoofd hebben door vragen te stellen.
Met vaste instructies en precieze stappenplannen lossen geprogrammeerde apparaten vraagstukken snel en effectief op. Als je weet dat in technologie deze routines zijn toegepast, helpt je dat beter begrijpen hoe een apparaat werkt.
De kinderen dagen akinator graag uit en hopen dat hij een keer de mist in gaat. Maar weten ze ook hoe akinator het raadt?
Bij jonge kinderen kun je ook al denken aan eenvoudige voorlopers van algoritmen, zoals het sorteren van blokjes van klein naar groot of het in volgorde vertellen bij dagritmekaarten.
Om een algoritme te kunnen bedenken, moet je wel eerst een patroon herkennen. Bij patroonherkenning noemden we als voorbeeld een ruzie op het plein. Als kinderen een patroon herkennen in de ruzies, zouden we ze ook kunnen uitdagen om een algoritme te bedenken voor het goed oplossen ervan.
Kunnen ze van dit ingewikkelde, sociale proces een stroomschema maken?
Abstractie
Abstractie komt van het Latijnse woord Abstraheren, wat ‘weglaten’ betekent. Het is het denkproces waarbij je boven de concrete werkelijkheid uitstijgt en bedenkt welke onderdelen essentieel zijn en welke je weglaat.
Zo maakte Plato onderscheid tussen de concrete, waarneembare en veranderlijke wereld van alledag, en de in zijn ogen ‘echte’ werkelijkheid, die bestaat uit abstracties, onveranderlijk is, en waarin ruimte en tijd niet bestaan.

Afbeelding 7: Een rode bal is een afspiegeling van twee vormaspecten: de kleur ‘rood’ en de vorm ‘rond’. Iedere bal maakt deel uit van de abstractie ‘bal’. Of de bal groot of klein is, in een bak ligt bij andere ballen of los op de grond ligt, in de lucht zweeft of over de grond rolt, dat maakt niet uit voor de abstractie ‘bal’.
Om abstractie te bereiken stelde Plato de vraag ‘Wat zijn fundamentele dingen waaruit de werkelijkheid bestaat?’ En dat is ook de vraag die ICT ontwikkelaars zichzelf stellen. Ze vormen een model van alle activiteiten, componenten en informatie die relevant is voor het te bouwen systeem.
Bijvoorbeeld voor het ventilatiesysteem in een auto is de temperatuursensor op de motor essentieel.
Abstractie in de klas

Afbeelding 8: In de onderbouw zijn de abstracties nog enkelvoudig en zichtbaar.
In de onderbouw oefenen kinderen al om voorwerpen te herkennen naar bijvoorbeeld vorm. Ze leren dat zowel een sinaasappel als een pizza cirkels zijn, ook al is de ene vorm bol en de ander plat.
Kinderen maken al vrij snel kennis met abstracties als het tekenen van een som of het maken van een woordweb.
In de midden- en bovenbouw kunnen kinderen steeds complexere situaties abstraheren, waarbij zij ook de onderlinge relaties tussen de essentiële onderdelen laten zien.
Bijvoorbeeld de kinderen van groep 8 maken een schema van het James Bond spel met afgooiers en balophalers, schuilplaatsen en thuisbasis, roofobjecten en puntentelling.
Decompositie
Sommige problemen of vraagstukken zijn zo complex, dat je ze niet op kunt lossen. Als je het probleem opdeelt in een heel veel kleine problemen, kun je die één voor één oplossen. En uiteindelijk heb je dan het grote probleem ook opgelost. Dit proces is decompositie.
Het groene laken

Afbeelding 9
Programmeur Wim Ligtendag noemt decompositie ‘het groene laken’, het operatiekleed met één klein gaatje erin. Een term die hij en zijn compagnon Ynze Baumfalk gebruiken om uit te leggen dat je het grootste deel van het probleem afdekt, op één stukje na. Dit stukje ga je goed bestuderen en oplossen.
Dit lijkt misschien een lastig onderdeel om in de klas te oefenen. Toch is decompositie te verbinden aan concrete voorwerpen en situaties. Om dit te illustreren, ziet u hier een paar leerdoelen voor decompositie uit de leerlijn ‘Denken als een programmeur’.
.jpg)
Afbeelding 10
Data en classificatie
Het laatste onderdeel van de leerlijn heeft betrekking op het leren herkennen van typen data en het ordenen van die gegevens in groepen.
Dit zullen leerkrachten in de onderbouw meteen herkennen. Met kleuters wordt er volop gegroepeerd en gesorteerd, bijvoorbeeld figuren van dezelfde vorm of kleur bij elkaar leggen, boerderij en wilde dieren onderscheiden en kleding en voorwerpen bij seizoenen sorteren.
Complexere vormen van ordenen
Bij de oudere kinderen kan het accent verlegd worden naar het zelf bedenken van categorieën waarmee dingen gesorteerd kunnen worden, naar andere typen data (bijvoorbeeld waar/ niet waar) en naar complexere vormen van ordenen.
Een voorbeeld hiervan is het ordenen van objecten op meerdere kenmerken; één object behoort dan tot meerdere groepen.

Afbeelding 11: Het ordenen van objecten op meerdere kenmerken is vergelijkbaar met de Matroesjka poppetjes. Eén poppetje past in één of meerdere andere poppetjes, die meer kunnen omvatten.
Objecten
Andersom is het mogelijk om met kinderen te kijken naar de abstracte vormen van objecten. Bijvoorbeeld: ‘Een kat en een koe zijn beide zoogdieren.’
Alles wat geldt voor een zoogdier, is van toepassing op zowel de kat als het zoogdier: ‘Zoogdieren zijn warmbloedig, dus een kat een koe zijn warmbloedig.’ Een zoogdier is een abstract object, het bestaat niet zelfstandig.

Afbeelding 12
Classificeren

Afbeelding 13: Hoe begin je met een puzzel? Sorteer je puzzelstukjes op kleur? Of haal je misschien de kantstukjes eruit? Classificeren heeft veel raakvlakken met organiseren. Je bedenkt voor het ordenen al wat een handige indeling is, afhankelijk van wat er uiteindelijk mee gedaan gaat worden.
Het meest duidelijk is deze vergelijking door te denken aan je digitale postvak en agenda. Deze staan vol mogelijkheden om je berichten, afspraken en taken te classificeren: met gekleurde vlaggen, vaste en zelfbedachte categorieën, taken, herinneringen. Dit heeft alleen zin als je vooraf bedenkt wat voor jou een handige manier is die je uiteindelijk helpt om je taken beter en op tijd te doen.
Voor de een betekent dit dat aan alle afspraken op de andere schoollocatie een herinnering toegevoegd wordt 15 minuten van tevoren in verband met de reistijd. Voor de ander betekent dit dat alle privé afspraken een oranje markering krijgen, en de werkafspraken blauw.
Leren denken als een programmeur
In dit artikel heb je kennis kunnen maken met een vijftal denkprocessen die essentieel zijn voor het werk van een programmeur:
- patroonherkenning
- algoritmen
- decompositie
- abstractie
- data en classificatie
De leerdoelen uit de leerlijn ‘Denken als een programmeur’ kunnen verrijkend zijn voor het leren.
Leestip deel 1: digitale bouwvakkers
Ook al worden leerlingen niet allemaal zelf een digitale bouwvakker, als zij begrijpen hoe een programmeur denkt, zijn zij beter in staat om te begrijpen hoe digitale oplossingen in elkaar zitten. En als het nodig is, kunnen zij gereedschap van de programmeur lenen om complexe vraagstukken op te lossen. Door te denken als een programmeur.

Afbeelding 14
Met dank aan Wim Ligtendag (GISfabriek) en Jan Geert Hek (Qtopia).
Bronnen
- Akinator. http://nl.akinator.com/
- BBC Bitesize (2015). Introduction to computational thinking. http://www.bbc.co.uk/education/topics/z7tp34j
- Benedictus, R. (2013). Plato, Socrates en de abstracte werkelijkheid. IsGeschiedenis. Verkregen op 8 december 2015 via http://www.isgeschiedenis.nl/filosofen/plato-socrates-en-de-abstracte-werkelijkheid/
- Berry, M. (2013). Computing in the national curriculum. A guide for primary teachers. Computing at school/Naace. Verkregen op 22 september 2015 via http://www.computingatschool.org.uk/data/uploads/CASPrimaryComputing.pdf.
- Computer Science Teachers Association (CSTA) and the International Society for Technology in Education (ISTE) (2011). Computational thinking. Teacher recourses. Verkregen op 14 oktober 2015 via http://csta.acm.org/Curriculum/sub/CurrFiles/472.11CTTeacherResources_2ed-SP-vF.pdf.
- Computing at school (2015). Computational thinking. How do we think about problems so that computers can help? Verkregen op 14 oktober 2015 via http://primary.quickstartcomputing.org/resources/pdf/comp_thinking.pdf
- Computing at school working Group (2014). Developing computational thinking in the classroom: a framework. Verkregen op 30 oktober 2015 via http://academy.bcs.org/sites/academy.bcs.org/files/DevelopingComputationalThinkingInTheClassroomaFramework.pdf.
- Computing at school working group (2012). Computer science: a curriculum for schools. Verkregen op 26 oktober 2015 via http://www.computingatschool.org.uk/data/uploads/ComputingCurric.pdf.
- Loesje. www.loesje.nl
- Pijpers, R. (2015). Computing-onderwijs in de praktijk. Wat kunnen we leren van de Britten? Kennisnet. Verkregen op 14 oktober 2015 via https://www.kennisnet.nl/fileadmin/kennisnet/publicatie/Computing_onderwijs_in_de_praktijk.pdf.
- Platform onderwijs 2032 (2015). Hoofdlijn advies: Een voorstel. Verkregen op 14 oktober 2015 via http://onsonderwijs2032.nl/wp-content/uploads/2015/09/Hoofdlijn-advies-Een-voorstel-Onderwijs2032.pdf.
- Wing, J.M. (2008). Computational thinking and thinking about computing. Phil. Trans. R. Soc. A 366, vbp. 3717–3725. Verkregen op 14 oktober 2015 via http://www.cs.cmu.edu/~wing/publications/Wing08a.pdf.
- Wing, J.M. (2006). Computational thinking. Communications of the ACM 49 (3), p. 33–35. Verkregen op 14 oktober 2015 via https://www.cs.cmu.edu/~15110-s13/Wing06-ct.pdf.